

انحراف مطلق
من ويكيبيديا،
في علم الإحصاء، الانحراف المطلق لإي عنصر ضمن مجموعة البيانات الإحصائية هو الفرق المطلق (القيمة المطلقة للفرق) بين هذا العنصر وقيمة أخرى معطاة.
عادة تكون هذه القيمة المعطاة هي المتوسط الحسابي أو الوسيط لمجموعة البيانات.
تعريف رياضي
يحسب الانحراف المطلق بالعلاقة: | D | = | x i − m ( X ) | {\displaystyle |D|=|x_{i}-m(X)|}
حيث: | D | {\displaystyle |D|} 


ــــــــــــــــــ
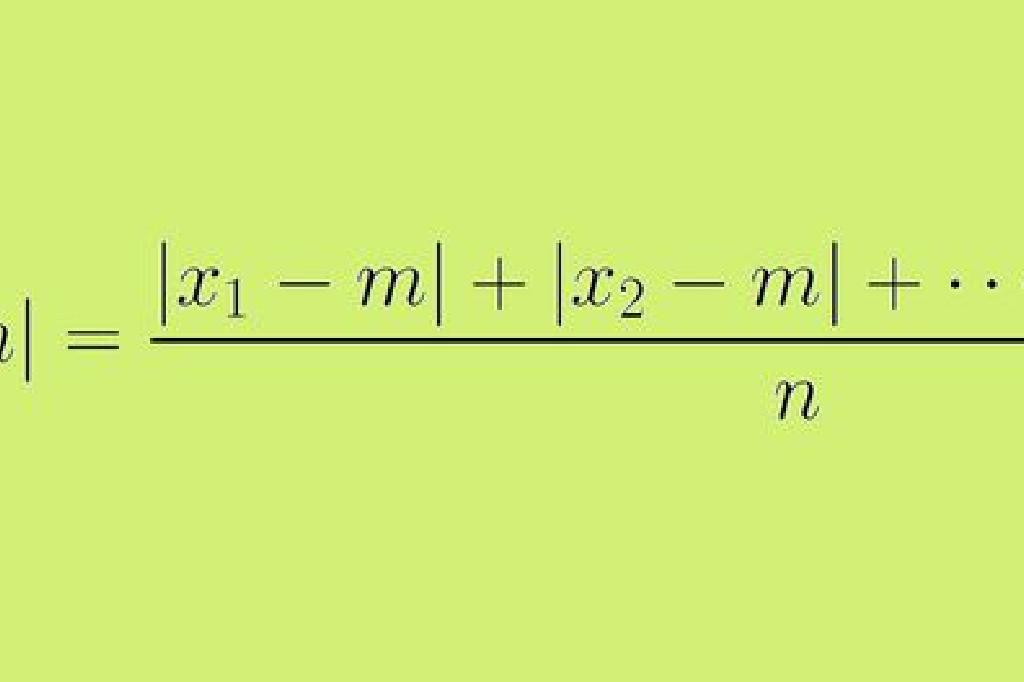
هناك العديد من قياسات الانتشار أو التشتت في الإحصائيات. على الرغم من أن النطاق والانحراف المعياري هما الأكثر استخدامًا ، إلا أن هناك طرقًا أخرى لقياس التشتت. سننظر في كيفية حساب متوسط الانحراف المطلق لمجموعة البيانات.
فريف
نبدأ بتعريف متوسط الانحراف المطلق ، والذي يشار إليه أيضًا باسم متوسط الانحراف المطلق. الصيغة المعروضة في هذه المقالة هي التعريف الرسمي لمتوسط الانحراف المطلق.
قد يكون من الأفضل التفكير في هذه الصيغة كعملية أو سلسلة من الخطوات التي يمكننا استخدامها للحصول على إحصائية.
- نبدأ بمتوسط ، أو قياس للمركز ، لمجموعة بيانات ، والتي سنشير بها م.
- بعد ذلك نجد مقدار انحراف كل من قيم البيانات عن m. هذا يعني أننا نأخذ الفرق بين كل من قيم البيانات و m.
- بعد ذلك ، نأخذ القيمة المطلقة لكل فارق من الخطوة السابقة. بعبارة أخرى ، نترك أي إشارات سلبية لأي اختلاف. سبب القيام بذلك هو أن هناك انحرافات إيجابية وسلبية من م. إذا لم نكتشف طريقة لإزالة العلامات السلبية ، فكل الانحرافات ستلغي بعضها البعض إذا أضفناها معًا.
- الآن نضيف معا كل هذه القيم المطلقة.
- وأخيرًا ، نقسم هذا المجموع على n ، وهو العدد الإجمالي لقيم البيانات. والنتيجة هي متوسط الانحراف المطلق.
الاختلافات
هناك العديد من الاختلافات في العملية المذكورة أعلاه. لاحظ أننا لم نحدد بالضبط م . والسبب في ذلك هو أنه يمكننا استخدام مجموعة متنوعة من الإحصائيات لـ m. عادة ما يكون هذا هو مركز مجموعة البيانات الخاصة بنا ، وبالتالي يمكن استخدام أي من قياسات الاتجاه المركزي. ad
تعد القياسات الإحصائية الأكثر شيوعًا لمركز مجموعة البيانات هي المتوسط والوسيط والوضع.
وبالتالي يمكن استخدام أي منها على شكل m في حساب متوسط الانحراف المطلق. وهذا هو السبب في أنه من الشائع الإشارة إلى متوسط الانحراف المطلق عن متوسط أو متوسط الانحراف المطلق عن الوسيط. سنرى العديد من الأمثلة على ذلك.
مثال – متوسط الانحراف المطلق عن المتوسط
لنفترض أننا نبدأ بمجموعة البيانات التالية:
1 و 2 و 2 و 3 و 5 و 7 و 7 و 7 و 7 و 9.
متوسط مجموعة البيانات هذه هو 5. سوف ينظم الجدول التالي عملنا في حساب متوسط الانحراف المطلق عن المتوسط.
| قيمة البيانات | الانحراف عن المتوسط | القيمة المطلقة للانحراف |
| 1 | 1 – 5 = -4 | | -4 | = 4 |
| 2 | 2 – 5 = -3 | | -3 | = 3 |
| 2 | 2 – 5 = -3 | | -3 | = 3 |
| 3 | 3 – 5 = -2 | | -2 | = 2 |
| 5 | 5 – 5 = 0 | | 0 | = 0 |
| 7 | 7 – 5 = 2 | | 2 | = 2 |
| 7 | 7 – 5 = 2 | | 2 | = 2 |
| 7 | 7 – 5 = 2 | | 2 | = 2 |
| 7 | 7 – 5 = 2 | | 2 | = 2 |
| 9 | 9 – 5 = 4 | | 4 | = 4 |
| مجموع الانحرافات المطلقة: | 24 |
نقوم الآن بتقسيم هذا المجموع على 10 ، حيث أن هناك إجمالي 10 قيم للبيانات. متوسط الانحراف المطلق للمتوسط هو 24/10 = 2.4.
مثال – متوسط الانحراف المطلق عن المتوسط
الآن نبدأ بمجموعة بيانات مختلفة:
1 ، 1 ، 4 ، 5 ، 5 ، 5 ، 5 ، 7 ، 7 ، 10.
تمامًا مثل مجموعة البيانات السابقة ، فإن متوسط مجموعة البيانات هذه هو 5.
| قيمة البيانات | الانحراف عن المتوسط | القيمة المطلقة للانحراف |
| 1 | 1 – 5 = -4 | | -4 | = 4 |
| 1 | 1 – 5 = -4 | | -4 | = 4 |
| 4 | 4 – 5 = -1 | | -1 | = 1 |
| 5 | 5 – 5 = 0 | | 0 | = 0 |
| 5 | 5 – 5 = 0 | | 0 | = 0 |
| 5 | 5 – 5 = 0 | | 0 | = 0 |
| 5 | 5 – 5 = 0 | | 0 | = 0 |
| 7 | 7 – 5 = 2 | | 2 | = 2 |
| 7 | 7 – 5 = 2 | | 2 | = 2 |
| 10 | 10 – 5 = 5 | | 5 | = 5 |
| مجموع الانحرافات المطلقة: | 18 |
ad
وبالتالي فإن متوسط الانحراف المطلق عن المتوسط هو 18/10 = 1.8. نحن نقارن هذه النتيجة بالمثال الأول. على الرغم من أن المتوسط كان متماثلاً لكل من هذه الأمثلة ، فإن البيانات في المثال الأول كانت أكثر انتشارًا. ونرى من هذين المثالين أن متوسط الانحراف المطلق عن المثال الأول أكبر من متوسط الانحراف المطلق عن المثال الثاني. كلما زاد متوسط الانحراف المطلق ، زاد تشتت بياناتنا.
مثال – متوسط الانحراف المطلق عن الوسيط
ابدأ باستخدام نفس مجموعة البيانات كمثال أول:
1 و 2 و 2 و 3 و 5 و 7 و 7 و 7 و 7 و 9.
متوسط مجموعة البيانات هو 6. في الجدول التالي نعرض تفاصيل حساب متوسط الانحراف المطلق حول الوسيط.
| قيمة البيانات | الانحراف عن الوسيط | القيمة المطلقة للانحراف |
| 1 | 1 – 6 = -5 | | -5 | = 5 |
| 2 | 2 – 6 = -4 | | -4 | = 4 |
| 2 | 2 – 6 = -4 | | -4 | = 4 |
| 3 | 3 – 6 = -3 | | -3 | = 3 |
| 5 | 5 – 6 = -1 | | -1 | = 1 |
| 7 | 7 – 6 = 1 | | 1 | = 1 |
| 7 | 7 – 6 = 1 | | 1 | = 1 |
| 7 | 7 – 6 = 1 | | 1 | = 1 |
| 7 | 7 – 6 = 1 | | 1 | = 1 |
| 9 | 9 – 6 = 3 | | 3 | = 3 |
| مجموع الانحرافات المطلقة: | 24 |
مرة أخرى ، نقوم بتقسيم الإجمالي على 10 ، ونحصل على متوسط متوسط الانحراف حول الوسيط على أنه 24/10 = 2.4.
مثال – متوسط الانحراف المطلق عن الوسيط
ابدأ باستخدام نفس مجموعة البيانات كما في السابق:
1 و 2 و 2 و 3 و 5 و 7 و 7 و 7 و 7 و 9.
في هذه المرة نجد أن وضع مجموعة البيانات هذه هو 7. في الجدول التالي ، نعرض تفاصيل حساب متوسط الانحراف المطلق عن الوضع.
| البيانات | الانحراف عن الوضع | القيمة المطلقة للانحراف |
| 1 | 1 – 7 = -6 | | -5 | = 6 |
| 2 | 2 – 7 = -5 | | -5 | = 5 |
| 2 | 2 – 7 = -5 | | -5 | = 5 |
| 3 | 3 – 7 = -4 | | -4 | = 4 |
| 5 | 5 – 7 = -2 | | -2 | = 2 |
| 7 | 7 – 7 = 0 | | 0 | = 0 |
| 7 | 7 – 7 = 0 | | 0 | = 0 |
| 7 | 7 – 7 = 0 | | 0 | = 0 |
| 7 | 7 – 7 = 0 | | 0 | = 0 |
| 9 | 9 – 7 = 2 | | 2 | = 2 |
| مجموع الانحرافات المطلقة: | 22 |
ad
نقسم مجموع الانحرافات المطلقة ونرى أن لدينا انحرافًا مطلقًا عن النمط 22/10 = 2.2.
حقائق عن متوسط الانحراف المطلق
هناك بعض الخصائص الأساسية فيما يتعلق بالانحرافات المطلقة
- دائمًا ما يكون متوسط الانحراف المطلق عن الوسيط أقل أو يساوي متوسط الانحراف المطلق عن المتوسط.
- يكون الانحراف المعياري أكبر من أو يساوي متوسط الانحراف المطلق عن المتوسط.
- أحيانًا ما يتم اختصار متوسط الانحراف المطلق بواسطة MAD. لسوء الحظ ، يمكن أن يكون هذا أمرًا غامضًا حيث أن MAD قد يشير بالتناوب إلى الانحراف المطلق المتوسط.
- متوسط الانحراف المطلق للتوزيع الطبيعي هو 0.8 ضعف حجم الانحراف المعياري تقريباً.
استخدامات الانحراف المطلق
متوسط الانحراف المطلق لديه بعض التطبيقات. التطبيق الأول هو أنه يمكن استخدام هذه الإحصائية لتعليم بعض الأفكار وراء الانحراف المعياري.
يكون من السهل حساب متوسط الانحراف المطلق للمتوسط عن الانحراف المعياري. إنه لا يتطلب منا أن نضبط الانحرافات ، ولا نحتاج إلى إيجاد جذر تربيعي في نهاية حساباتنا. علاوة على ذلك ، فإن متوسط الانحراف المطلق مرتبط بشكل حدسي بانتشار مجموعة البيانات أكثر من الانحراف المعياري. وهذا هو السبب في أنه يتم تدريس الانحراف المطلق في بعض الأحيان أولاً ، قبل إدخال الانحراف المعياري.
وقد ذهب البعض إلى حد القول بأن الانحراف المعياري ينبغي استبداله بالاختصار المطلق. على الرغم من أن الانحراف المعياري مهم للتطبيقات العلمية والرياضية ، إلا أنه ليس بديهيًا مثل متوسط الانحراف المطلق. بالنسبة للتطبيقات اليومية ، فإن متوسط الانحراف المطلق هو طريقة أكثر واقعية لقياس مدى انتشار البيانات.



