
ليوناردو فيبوناتشي
من ويكيبيديا،
ليوناردو فيبوناتشي (بيزا، 1175م – 1250م) هو عالم رياضيات إيطالي؛ من أبرز رياضياتي العصور الوسطى في أوروبا. كان يعرف فيما مضى باسم ليوناردو بيزانو (نسبة إلى مدينته بيزا)، كما كان يعرف باسم ليوناردو بيغولو (وتعني Bigollo المسافر)، لكن اسمه الحقيقي كان ليوناردو غيلييلمي (بالإيطالية: Leonardo Gulielmi) وقد اشتهر حديثا باسم فيبوناتشي، الذي يعني ابن بوناتشي (filius Bonaccio)، الاسم الذي تعلّق به بعد وفاته.
عرف العالم فيبوناتشي بمساهمته في نشر “الأرقام العربية” في أوروبا، خاصة ضمن كتابه الذي نشره في القرن الثالث عشر بعنوان ليبر أباتشي (باللاتينية: Liber Abaci)؛ يترجم عنوان هذا الكتاب إلى كتاب الحساب. وكذلك عُرف بمتتالية فيبوناتشي التي سميت نسبة إليه، والتي ذكرها مثالاً في كتابه المذكور.
السيرة الذاتية:

تمثال من القرن التاسع عشر لفيبوناتشي في كامبوسانتو، بيزا
ولد فيبوناتشي في مدينة بيزا بإيطاليا حوالي عام 1170 م لوالده جوجلييلمو فيبوناتشي، تاجر إيطالي غني. وقد تلقى ليوناردو تعليمه بالأساس في مدينة بجاية الجزائرية. وقد كان والده قيلييلمو بوناتشي مشرفا على أسواق بيزا في الجزائر و تونس والمغرب، [7]
وقد جلب فيبوناتشي من هذه الأماكن، حسبما قيل، سنة 1200، الأرقام العربية المستعملة اليوم والعلامات الجبرية وقد قيل أيضا أن من قام بذلك كان جيربير دوريلاك. وفي سنة 1202، أصدر كتابا بعنوان “ليبر أباشي”، المتخصص في الحساب والمحاسبة.
وقد تأثر فيبوناتشي في هذا الكتاب بحياته في الدول العربية، ومما يدلّ على ذلك أن فبيوناتشي قد قام بتحرير جزء منه من اليمين إلى اليسار. وبنشر هذا الكتاب قام فيبوناتشي بتعريف الأوروبيين على أنظمة الحساب والكتابة العربية. وقد كان هذا النظام يفوق بمراحل النظام الروماني المعتمد آنذاك في أوروبا، وكان فيبوناتشي على دراية بذلك. لكن هذا النظام واجه عنتا كبيرا قبل أن ينتشر بصورة عظيمة.
و قد اشتهر فيبوناتشي أساسا بسيبب مسألة تقودنا إلى متتالية فيبوناتشي، ولكنه عرف فيما مضى بسبب تطبيقه للأريثماطيقية على الحساب التجاري : حساب الأرباح، تحويل العملات.. لكن أعماله المتعلقة بنظرية الأعداد أهملت في حياته. وفي دراسة صغيرة أجريت حوله لاحقاـ تم اكتشاف طرائق خفية كان يستعملها نجدها حتى في بعض جوانب البورصة (التحليل التقني). واسم فيبوناتشي الذي يعني ابن بوناتشي تعلّق به بعد وفاته.
في القرن التاسع عشر، تم بناء تمثال لفيبوناتشي ووضع في بيزا. اليوم التمثال موجود في المعرض الغربي في كامبوسانتو، بيزا.
مؤلفاته
Liber abbaci, MS Biblioteca Nazionale di Firenze, Codice Magliabechiano cs cI 2616, fol. 124r
له هذه الكتب التي نشرها المؤرخ الإيطالي المختص في تاريخ الرياضيات بلتزار باكومبانيي (بالإيطالية: Baldassare Boncompagni), فلورنسا, 1854 :
- ليبر أباتشي أُلف سنة 1202. وذكر فيه أنه تعلم في مدرسته الرياضيات ولأول مرة الرموز الهندية التسعة (وهي أصلا عربية). هذا الكتاب نرى التأثيرات العربية عبر كتابته الكثير من الأرقام من اليمين إلى اليسار.
- Practice Geometion :الف سنة 1228 عرض فيه حلاً لمسائل رياضية كثيرة.
- Libre Quardratorum : الف سنة 1225 يعتبر من أهم مؤلفاته واسمه كتاب المربعات. تم فيه اختيار الكثير من المسائل الرياضية المهمة ومن ضمنها الحصول على المضاعف الثلاثي لفيثاغورس.
- Quadrati numeri.
متتالية فيبوناتشي
- لو اعتبرنا {\displaystyle {\mathcal {F}}_{n}}
العنصر n للمتوالية الرياضية، فإن{\displaystyle \forall n\in \mathbb {W} ,{\mathcal {F}}_{n+2}={\mathcal {F}}_{n+1}+{\mathcal {F}}_{n}}
و {\displaystyle {\mathcal {F}}_{1}=1,{\mathcal {F}}_{2}=1}
(نعتبر {\displaystyle {\mathcal {F}}_{0}=0}
).
و من بعض خصائص هذه المتتالية، أن خارج قسمة اي عنصر على العنصر الذي قبله يقترب رويدا رويدا من الرقم الذهبي, المعرف بـ :
{\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}\simeq 1,6180339887…}
من تعريف المتوالية ممكن أن نرى أن المتوالة تبدأ بالحدود التالية: 1 ،1، 2، 3، 5، 8، 13، 21، 34، 55، 89، 144، 233، 377، 610، 987…
و نعرّف كذلك {\displaystyle {\mathcal {L}}_{n}}




من ويكيبيديا
في الرياضيات، متتالية فيبوناتشي أو أعداد فيبوناتشي (بالإنجليزية: Fibonacci numbers) نسبة إلى عالم الرياضيات الإيطالي ليوناردو فيبوناتشي، هي متتالية يساوي فيها الحد مجموع الحدين السابقين.
حدود هذه المتتالية الأولى هن الأعداد التالية:

تبليط المربعات حيث يكون الجانبان هما أعداد فيبوناشي المتتالية في الطول
يوبانا [الإنجليزية] (وتعني بالكيشوا أداة عد) وهي آلة حسابية استخدمها الإنكا. يعتقد الباحثون بأن تلك الحسابات اعتمدت على أعداد فيبوناشي لتقليل عدد الحبوب اللازمة لكل حقل.[1]
لولب فيبوناتشي بطريقة رسم أقواس متصلة بالزوايا المتقابلة من المربعات في تبليط فيبوناتشي، ويستخدم لأحجام المربعات التالية 1، 1، 2، 3، 5، 8، 13، 21، 34، انظر الدوامة الذهبية [الإنجليزية]
تعرف المتتالية {\displaystyle F_{n}}
 لعدد فيبوناتشي بالوصف الرياضياتي مستعملا علاقة استدعاء ذاتي :
لعدد فيبوناتشي بالوصف الرياضياتي مستعملا علاقة استدعاء ذاتي :{\displaystyle F_{n}=F_{n-1}+F_{n-2},\!\,}

مع القيم الناتجة عنها
{\displaystyle F_{0}=0}
 و {\displaystyle F_{1}=1}
و {\displaystyle F_{1}=1}
سميت متتالية فيبوناتشي نسبة إلى ليوناردو البيسي والمعروف باسم فيبوناتشي (باللاتينية: Fibonacci). عرف هذا العالم هذه المتتاليه في كتاب له اسمه ليبري أباتشي نشره عام 1202، رغم أنها كانت معروفة وموصوفة بالسابق في الرياضيات الهندية.[2][3]
متتالية فيبوناتشي مرتبطة ارتباطا شديدا بالنسبة الذهبية. تعبر صيغة بِينيت عن حد متتالية فيبوناتشي من الدرجة n مستعملة n ذاته إضافة إلى النسبة الذهبية، ومبينة أن النسبة بين حدين متتابعين من المتتالية تؤول إلى النسبة الذهنية عندما يؤول n إلى ما لا نهاية له.
ترتبط أعداد فيبوناتشي أيضا بأعداد لوكاس {\displaystyle L_{n}}
 ، كونهما تكونان زوجا متكاملا من متتالية لوكاس : {\displaystyle U_{n}(1,-1)=F_{n}}
، كونهما تكونان زوجا متكاملا من متتالية لوكاس : {\displaystyle U_{n}(1,-1)=F_{n}} و {\displaystyle V_{n}(1,-1)=L_{n}}
و {\displaystyle V_{n}(1,-1)=L_{n}} .
.محتويات
1التاريخ
2تطبيقات
3في الرياضيات3.1خصائص المتتالية وقيمها
3.2علاقتها بالنسبة الذهبية
3.3الصيغة العامة
3.4متسلسلات القوى
4علاقتها بمسألة سيراكيز
5انظر أيضا
6مصادر
التاريخ[عدل]
انظر أيضا تاريخ النسبة الذهبية.
صفحة من الكتاب ليبر أباتشي لفيبوناتشي الموجود في المكتبة الوطنية المركزية في فلورنسا مبينا (في العلبة يمينا) متتالية فيبوناتشي مع موقع الحد في المتتالية مشارا إليه بالأعداد اللاتينية والرومانية وبالأرقام العربية الهندية.
عرف الهنود القدماء متتالية فيبوناتشي قبل ظهورها في أوروبا، حيث طبقوها في علم أوزان الشعر.[4]
وجاء الدافع لذلك من العروض السنسكريتية، حيث المقاطع الطويلة لها فترة = 2 والمقاطع القصيرة لها فترة = 1. يمكن تشكيل أي نمط له فترة ن وذلك بإضافة مقطع قصير إلى نمط من فترة ن − 1، أو مقطع طويل لنمط من فترة ن − 2 ، وبالتالي فإن عروض الشعر تظهر أن عدد أنماط فترة ن هو مجموع الرقمين السابقين من التسلسل. وبعد ذلك بدأ المؤلفون باستخدام الخوارزميات لتصنيف أو عدم تصنيف تلك الأنماط (بمعنى إيجاد النمط المرقم بالكاف من الفترة ن)، مما أدى لاكتشاف أرقام فيبوناتشي عليا. وقد استعرض دونالد كانوث تلك النتيجة في كتابه فن برمجة الحاسوب.[5][6]
وقد بدأ ليوناردو البيسي المعروف باسم فيبوناتشي بدراسة تلك المتتالية في أوروبا في كتابه ليبر أباتشي (1202).[7] واعتبر النمو على افتراض (وهو غير صحيح في علم الأحياء) مجموعة ارانب كالتالي: حقل به زوج من الأرانب حديثي الولادة إحداهما ذكر والآخر انثى، فالأرانب بإمكانها التزاوج عند بلوغ الشهر، لذا ففي نهاية الشهر التالي تكون الأنثى قد ولدت زوج من الأرانب؛ بافتراض أنه لم يمت أي أرنب خلال مدة معينة وبافتراض أن في كل شهر ينتج زوج من الأرانب (ذكر وأنثى) بدأ من الشهر التالي. فكان اللغز الذي طرحه فيبوناتشي هو: كم سيكون عدد الأزواج في السنة الواحدة؟
في نهاية الشهر الأول سيحصل تزاوج، ولكن يبقى أن هناك زوجا واحدا فقط.
في نهاية الشهر التالي، الأنثى تلد زوجا جديدا، لذا سيكون هناك زوجين من الأرانب في الحقل.
في نهاية الشهر الثالث، الأنثى الأصل تلد زوجا جديدا، مما يصبح العدد هو 3 أزواج من الأرانب في الحقل.
في نهاية الشهر الرابع تلد الأُنثى الأصل زوجا من الأرانب، والأنثى التي ولدت قبل شهرين تلد أول زوج لها من الأرانب. مما يصبح العدد هو 5 أزواج.
وفي نهاية المطاف عند الشهر ن، عدد الأزواج من الأرانب يساوي عدد الأزواج المواليد (حيث هو عدد الأزواج في الشهر ن-2) زائد عدد الأزواج الأحياء عند آخر شهر. هذا هو أو العدد ن لمتتالية فيبوناتشي.[8]
تطبيقات[عدل]
استخدمت متتالية فيبوناتشي في تحليل الأسواق المالية وفي استراتيجيات مثل ارتداد فيبوناتشي وفي خوارزميات االكمبيوتر مثل تقنية فيبوناتشي للبحث وهيكلة بيانات تكدس فيبوناتشي [الإنجليزية]. وهي تظهر أيضا في الترتيبات البيولوجية[9]، مثل تفريعات الأشجار وترتيب الأوراق على الساق وطرف الثمرة من الأناناس[10] وتفتح الخرشوف والسرخس غير المتجعد وترتيب مخروط الصنوبر.[11]
تمكن عالم الرياضيات الروسي يوري ماتياسفيتش من البرهان على أن أعداد فيبوناتشي يمكن أن تعرف بمعادلة ديفونتية. فتح له ذلك باب برهان معضلة هيلبرت العاشرة.
متتالية فيبوناتشي هي مثال عن المتتاليات الكاملة. هذا يعني أن كل عدد صحيح طبيعي يمكن أن يكتب مجموعا لأعداد فيبوناتشي بدون استعمال أحد منهن أكثر من مرة.
تستعمل أعدادَ فيبوناتشي بعض مولدات الأعداد شبه العشوائية.
في الرياضيات[عدل]
أعداد فيبوناتشي هي المجاميع للأقطار المائلة السطحية المبينة باللون الأحمر في مثلث باسكال.
تظهر أعداد فيبوناتشي على شكل مجاميع في مثلث باسكال للأعداد الواقعة على أقطار مائلة (انظر إلى معامل ثنائي).
{\displaystyle F_{n}=\sum _{k=0}^{\left\lfloor {\frac {n-1}{2}}\right\rfloor }{\binom {n-k-1}{k}}.}

تظهر أعداد فيبوناتشي أيضا جوابا على معضلة معروفة في التحليل التوافقي والمتمثلة فيما يلي : كم عدد طرق كتابة عدد ما، مجموعا مرتبا من الرقمين الواحد والاثنين. الجواب هو Fn+1. على سبيل المثال، إذا كان n يساوي خمسة، فإن Fn+1 = F6 = 8
5 = 1+1+1+1+1 = 1+1+1+2 = 1+1+2+1 = 1+2+1+1 = 2+1+1+1 = 2+2+1 = 2+1+2 = 1+2+2.
خصائص المتتالية وقيمها[عدل]
أول 21 من أرقام فيبوناتشي (متسلسلة A000045 في OEIS)، ومرقمة بالعلامة Fن حيث ن = 0, 1, 2,… ,20 هي:[12][13]
F0
F1
F2
F3
F4
F5
F6
F7
F8
F9
F10
F11
F12
F13
F14
F15
F16
F17
F18
F19
F20
0
1
1
2
3
5
8
13
21
34
55
89
144
233
377
610
987
1597
2584
4181
6765
قد يبدو ملاحظا أن المرة 21 (13+34) تساوي 987. أو تلكم المرة 34 (21+55) تساوي 2584. باستخدام العلاقة المكررة يمكن للتسلسل أن يمتد إلى مؤشر سلبي ن. نتيجة ترضي المعادلة
فتكون المعادلة لتلك النتائج
{\displaystyle F_{-n}=(-1)^{n+1}F_{n}.\!\,}

وهذا التسلسل كاملا
{\displaystyle \ldots ,\;-8,\;5,\;-3,\;2,\;-1,\;1,\;0,\;1,\;1,\;2,\;3,\;5,\;8,\;\ldots }

علاقتها بالنسبة الذهبية[عدل]
 مقالة مفصلة: نسبة ذهبية
مقالة مفصلة: نسبة ذهبيةحاول العلماء أن يفهموا هذه السلسلة، فقاموا بقسمة كل حد على الحد السابق له، فاكتشفوا أن هذه المتتالية تنفرد بخصائص كثيرة منها العلاقة مع النسبة الذهبية، ذلك أنه إذا اعتُبرت قسمة كل عدد من المتتالية على العدد الذي يسبقه (1÷1=1 ، 1÷2=2 ، 2÷3=1.5 ، 3÷5=1.6666666 ، 5÷8=1.6، 8÷13= 1.625، 13÷21 = 1.61538، …) يُلاحظ الاقتراب شيئا فشيئا من الرقم 1.618034 الذي يسمى الرقم الذهبي نظرا لخصائصه العجيبة في الرياضيات كما في الطبيعة.
اطلق العلماء على الرقم الذهبي اسم “فاي” أو “في” (phi) وبعد محاولة التوصل إلى النسبة بين أربعين حدا متتاليا في متتالية فيبوناتشي وجدوا انه يمكن تقريب “فاي” إلى 15 رقم عشري
Φ = 1.618033988749895, …
تتكون النسبة الذهبية من عددين هما 1.618034 و 0.618034 وكلا العددين هو المقلوب الحسابي للعدد الأخر.
الصيغة العامة[عدل]
الصيغة العامة لمتتالية فيبوناتشي هي :{\displaystyle F(n)={\frac {1}{\sqrt {5}}}(\varphi ^{n}-\varphi ‘^{n})}
 مع :{\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}\,}
مع :{\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}\,} و{\displaystyle \varphi ‘={\frac {1-{\sqrt {5}}}{2}}\,}
و{\displaystyle \varphi ‘={\frac {1-{\sqrt {5}}}{2}}\,}
و هذه بعض القيم: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946,…
ويقترب ناتج قسمة كل رقم بما قبله من 1.618 شيئا فشيئا للرقم الذهبي ويسمى هذا الرقم أيضا برقم التناسب المقدس والنسبة الذهبية.
تسمى هذه الصيغة صيغة بينيت نسبة إلى عالم الرياضيات الفرنسي جاك فيليب ماري بينيه.
يمكن إثبات صحة الجملة العامة عن طريق الاستقراء الرياضي.[14]
الأساس: لنوضح أن التعبير صحيح من أجل {\displaystyle n=0}
 و {\displaystyle n=1}
و {\displaystyle n=1} :
:{\displaystyle F(0)={\frac {\left({\frac {1+{\sqrt {5}}}{2}}\right)^{0}-\left({\frac {1-{\sqrt {5}}}{2}}\right)^{0}}{\sqrt {5}}}={\frac {1-1}{\sqrt {5}}}=0}

{\displaystyle F(1)={\frac {\left({\frac {1+{\sqrt {5}}}{2}}\right)^{1}-\left({\frac {1-{\sqrt {5}}}{2}}\right)^{1}}{\sqrt {5}}}={\frac {{\frac {1+{\sqrt {5}}}{2}}-{\frac {1-{\sqrt {5}}}{2}}}{\sqrt {5}}}={\frac {\frac {1+{\sqrt {5}}-1+{\sqrt {5}}}{2}}{\sqrt {5}}}={\frac {\frac {{\sqrt {5}}+{\sqrt {5}}}{2}}{\sqrt {5}}}={\frac {\frac {2{\sqrt {5}}}{2}}{\sqrt {5}}}={\frac {\sqrt {5}}{\sqrt {5}}}=1}

خطوة الاستقراء : تبين أنه إذا كانت {\displaystyle F(n)}
 و {\displaystyle F(n-1)}
و {\displaystyle F(n-1)} صحيحة، فإن {\displaystyle F(n+1)}
صحيحة، فإن {\displaystyle F(n+1)} صحيحة أيضا. يتم ذلك على النحو الاتي.[14]
صحيحة أيضا. يتم ذلك على النحو الاتي.[14]{\displaystyle {\begin{aligned}F\left(k+1\right)&=F\left(k\right)+F\left(k-1\right)\\&={\frac {\left({\frac {1+{\sqrt {5}}}{2}}\right)^{k}-\left({\frac {1-{\sqrt {5}}}{2}}\right)^{k}}{\sqrt {5}}}+{\frac {\left({\frac {1+{\sqrt {5}}}{2}}\right)^{k-1}-\left({\frac {1-{\sqrt {5}}}{2}}\right)^{k-1}}{\sqrt {5}}}\\&={\frac {\left({\frac {1+{\sqrt {5}}}{2}}\right)^{k}+\left({\frac {1+{\sqrt {5}}}{2}}\right)^{k-1}-\left({\frac {1-{\sqrt {5}}}{2}}\right)^{k}-\left({\frac {1-{\sqrt {5}}}{2}}\right)^{k-1}}{\sqrt {5}}}\\&={\frac {\left(\left({\frac {1+{\sqrt {5}}}{2}}\right)+1\right)\left({\frac {1+{\sqrt {5}}}{2}}\right)^{k-1}-\left(\left({\frac {1-{\sqrt {5}}}{2}}\right)+1\right)\left({\frac {1-{\sqrt {5}}}{2}}\right)^{k-1}}{\sqrt {5}}}\\&={\frac {\left(\left({\frac {3+{\sqrt {5}}}{2}}\right)\right)\left({\frac {1+{\sqrt {5}}}{2}}\right)^{k-1}-\left(\left({\frac {3-{\sqrt {5}}}{2}}\right)\right)\left({\frac {1-{\sqrt {5}}}{2}}\right)^{k-1}}{\sqrt {5}}}\\&={\frac {\left(\left({\frac {1+{\sqrt {5}}}{2}}\right)^{2}\right)\left({\frac {1+{\sqrt {5}}}{2}}\right)^{k-1}-\left(\left({\frac {1-{\sqrt {5}}}{2}}\right)^{2}\right)\left({\frac {1-{\sqrt {5}}}{2}}\right)^{k-1}}{\sqrt {5}}}\\&={\frac {\left({\frac {1+{\sqrt {5}}}{2}}\right)^{k+1}-\left({\frac {1-{\sqrt {5}}}{2}}\right)^{k+1}}{\sqrt {5}}}\end{aligned}}}

متسلسلات القوى[عدل]
الدالة المولدة لمتتالية فيبوناتشي هي متسلسلة القوى التالية:
{\displaystyle s(x)=\sum _{k=0}^{\infty }F_{k}x^{k}.}

هذه المتسلسلة تتقارب حين يتوفر {\displaystyle |x|<{\frac {1}{\varphi }},}
 ولمجموعها شكل مغلق بسيط هو:
ولمجموعها شكل مغلق بسيط هو:{\displaystyle s(x)={\frac {x}{1-x-x^{2}}}}

علاقتها بمسألة سيراكيز[عدل]
مجموعة فيبوناتشي هي متتالية فيبوناتشي ولكنها بخلاف مجموعة من الأرقام لها صلات بالاعداد للكواكب والمجرات والتصنيفات النباتيه والحيوانيه ويقال عند الهنود القدماء قبل ظهور تلك المتتاليه ان هناك مجموعة من الاعداد ذات ترتيب معين له صلة باحداث يوميه في الحاضر والمستقبل متوقع حدوثها.

أعداد فيبوناتشي هي المجاميع للأقطار السطحية المبينة باللون الأحمر في مثلث باسكال.
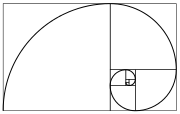
لولب فيبوناتشي بطريقة رسم أقواس متصلة بالزوايا المتقابلة من المربعات في تبليط فيبوناتشي، ويستخدم لأحجام المربعات التالية 1، 1، 2، 3، 5، 8، 13، 21، 34، انظر الدوامة الذهبية

يوبانا[الإنجليزية] (وتعني بالكيشوا أداة عد) وهي آلة حسابية استخدمها الإنكا. يعتقد الباحثون بأن تلك الحسابات اعتمدت على أعداد فيبوناشي لتقليل عدد الحبوب اللازمة لكل حقل.

تبليط المربعات حيث يكون الجانبان هما أعداد فيبوناشي المتتالية في الطول

يتجلى العدد في الطبيعة بأشكال مختلفة.



