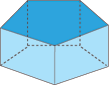
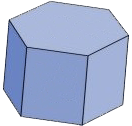
الموشور القائم : وصفه حجمه و مساحته الجانبية و الكلية

الموشور القائم هو مجسم يتشكل من قاعدتين متوازيتين و قابلتين للتطابق، وله احرف جانبية متقايسة كل منها يعتبر ارتفاع في الموشور القائم وله أوجه جانبية على شكل مستطيلات وهو أنواع منها : الموشور القائم الذي قاعدته مثلث والموشور القائم قاعدته مستطيل، الموشور القائم قاعدته مربع وهناك موشور قائم قاعدته مضلع خماسي أو سداسي ….إلخ.

الموشور القائم : و صف + تعريف.

الموشور القائم هو مجسم يتكون من :

1. وجهين متوازيين قابلين للتطابق هما : قاعدتان الموشور القائم .
2. أحرف جانبية متقايسة هي : ارتفاع الموشور القائم .
3. أوجه جانبية و هي على شكل : مستطيلات .

ملاحظات هامة :

• عدد الأوجه الجانبية لموشور قائم يساوي عدد أضلاع قاعدته .
• قاعدتا الموشور القائم إما أن تكونا على شكل مثلث أو مربع أو مستطيل أو مضلع رباعي أو مضلع خماسي ……….
• إذا كانت قاعدتا الموشور القائم عبارة عن مستطيلين فإن هذا الموشور يسمى متوازي المستطيلات.

• إذا كانت قاعدتا الموشور القائم عبارة عن مربع و كان الإرتفاع مساوي لطول حرف في المربع فإن هذا الموشور يسمى مكعب.

حجم الموشور القائم :

حجم الموشور القائم هو الحيز الذي يشغله هذا المجسم في الفضاء و نرمز له بالرمز V. و لحساب حجم أي موشور قائم نضرب مساحة قاعدته في ارتفاعه ، حيث القاعدة قد تكون عبارة عن مثلث أو مربع أو مستطيل أو خماسي……

حجم الموشور القائم = مساحة قاعدته × ارتفاعه
V  = b ×  h

مثال :
أسفله لدينا موشور قائم قاعدته عبارة عن مثلث قائم الزاوية . جد حجمه .

موشور قائم قاعدته  مثلث قائم الزاوية

الحل : 
حجم الموشور = مساحة قاعدته × ارتفاعه
القاعدة هنا عبارة عن مثلث قائم الزاوية إذن :  b = ( 5 × 12 ) ÷ 2 = 30  => b = 30cm²
أي أن :    V  = b ×  h = 30 × 10 = 300 => V = 300 cm3

مثال أخر :

باب من الخشب ارتفاعه 2 متر ، وعرضه 1 متر ، وسماكة الخشب المصنوع منه = 5 ستنمتر . بفرض أن الباب منتظم وعلى شكل متوازي مستطيلات ، فالمطلوب حساب حجم مادة الخشب التي صنع منها الباب .

الحل : 

متوازي المستطيلات هو موشور قائم بقاعدة مستطيلة الشكل ( مساحة المستطيل= جداء بعيديه )

حجم الباب = ارتفاعه × عرضه × سماكته = حجم الخشب المصنوع منه .

لاحظ هنا أن الأبعاد مختلفة في وحداتها فاثنان منها مقاسان بالمتر والثالث بالسنتمتر ، إذن عند حساب الحجم يجب جعل الوحدات كلها متشابهة .  5cm = 0.05m

V = 2 × 1 × 0.05 = 0.1m3

للتفكير :

 لو كان لدينا قطعة خشب على شكل متوازي مستطيلات أبعادها 2م × 1م × 1م ، فكم باباً من النوع المذكور في السؤال نستطيع أن نعمل منها بفرض أنه لن يضيع منها أي شيء أثناء عمليات القص والتشكيل .

المساحة الجانبية و الكلية للموشور القائم

للموشور القائم كما عرفنا قاعدتان وعدد من الأوجه يعتمد على شكل القاعدة ، فالموشورالقائم الثلاثي له ثلاثة أوجه مستطيلة (بالاضافة إلى قاعدتيه) ومتوازي المستطيلات له أربعة أوجه مستطيلة (بالاضافة إلى قاعدتيه وهما مستطيلتان ) والموشور القائم السداسي له ستة أوجه مستطيلة ……. إلخ.

كثيراً ما يطلب منا حساب مساحة هذه الأوجه مع أو بدون القاعدتين، ولذلك سنميز بين حالتين :

      قاعدة:

• مساحة سطح الموشور القائم الجانبية : هي مجموع مساحة أوجه الموشورالمستطيلة دون القاعدتين .
• مساحة سطح الموشور القائم الكلية : هي مجموع مساحة أوجه الموشور المستطيلة + مساحة القاعدتين .

المثال التالي يوضح ذلك :

مثال  : علبة من الورق المقوى على شكل موشور ثلاثي قائم أبعاده كما في الشكل :

AB = 3cm  ;;    AC = 4cm   ;;     BC= 5cm     ;;   BB’= 7cm

علبة من الورق المقوى على شكل موشور ثلاثي قائم

المطلوب :

أ‌ –  حساب مساحة الموشورالجانبية .

ب‌- حساب مساحة سطح الموشور الكلية .

الحـــل :

  أ –  جوانب هذا الموشور عبارة عن ثلاث مستطيلات :

• المستطيل’ABB’A ومساحته هي = الطول × العرض =>  S(ABB’A’) = 3 × 7 = 21 cm²
• المستطيل’AِCC’A ومساحته هي = الطول × العرض => S(AِCC’A’) = 4 × 7 = 28 cm² .
• المستطيل BB’C’C ومساحته هي = الطول × العرض =>  S(BB’C’C) = 5 × 7 = 35 cm²

إذن المساحة الجانبية لهذا الموشور القائم تكون هي مجموع المساحات الجزئية للجوانب و نكتب :

 84  = 21 + 28 + 35 = (S = S(ABB’A’) + S(AِCC’A’)  + S(BB’C’C

S = 84cm²

ويمكن اختصار هذه الطريقة حيث يمكن اعتبار السطح الجانبي للموشور تحول إلى مستطيل طوله يساوي محيط قاعدة الموشور= 4 + 3 + 5 = 12سم وعرضه هو ارتفاع الموشور = 7 سم ،
حيث يمكن حساب المساحة الجانبية = 12 × 7 = 84 سم2 .

وتصبح مساحة الموشور القائم الجانبية = محيط القاعدة × ارتفاع الموشور .

 ب‌ – مساحة السطح الكلية = المساحة الجانبية + مساحة القاعدتين .

إن قاعدة المنشور هي عبارة عن مثلث قائم الزاوية و بالتالي :

S(ABC) = ( 3 × 4 ) ÷ 2 = 6cm²

أيضا لدينا :

S(A’B’C’) = ( 3 × 4 ) ÷ 2 = 6cm²

إذن المساحة الكلية للموشور :

96 = 84 + 6 + 6 = S’ = S(ABC) + S(A’B’C’) + S

S’ = 96cm²

وعموماً المساحة الكلية = المساحة الجانبية + مساحة القاعدتين = ( محيط القاعدة × الارتفاع ) + ( ضعف مساحة القاعدة ).

ثالثا: المنشور الثلاثي Triangular Prism

وهو منشور قائم قاعدته مثلث وله ثلاث أوجه جانبية كل منها مستطيل . أمثلة : أوضح الأمثلة على هذا النوع موشورات تحليل الضوء وعادة ما تكون قاعدتها مثلث قائم الزاوية متساوي الساقين ، أو مثلت متساوي الأضلاع . أمثلة أخرى : بعض أنواع علب العصير قد تكون على شكل المنشورات الثلاثية .

 

	رابعا: الموشور الخماسي وهو موشوور قائم قاعدته خماسي منتظم أو غير منتظم Pentagonal Prism . وأشهر مثال لهذا النوع : هو وزارة الدفاع الأمريكية المعروفة باسم Pentagon نسبة لشكل بنائها.
	خامسا:الموشور السداسي : وهو موشور قاعدته سداسي منتظم أو غير منتظم Hexagonal Prism. مثال : أوضح مثالي طبيعي عليه هو بلورات المرو ( Quartz ) السداسية .

سادسا: حساب حجم الموشور عموماً مهما كان شكل قاعدته :
لحساب حجم أي منشور نضرب مساحة قاعدته في ارتفاعه ، حيث مساحة القاعدة تمثل حاصل ضرب بعدين من أبعاده ، ويكون الارتفاع هو البعد الثالث .

مثال : منشور سداسي قائم مساحة قاعدته 60 سم² وارتفاعه 12 سم . جد حجمه .

الحل : حجم المنشور = مساحة قاعدته × ارتفاعه

= 60 سم² × 12 سم = 720 سم³ .

موشور (بصريات)

في البصريات الموشور أو المنشور هو وسط شفاف مثل الزجاج، محدود بوجهين مستويين يتقاطعان حسب مستقيم يسمى حرف الموشور، قاعدة الموشور هي الوجه المقابل للحرف.

زاوية الموشور (A) هي الزاوية المقابلة للقاعدة. ويرجع السبب في تحلل الضوء الأبيض إلى ألوانه المختلفة أثناء مروره داخل الموشور إلى اختلاف سرعة الضوء في مادة المنشور عن سرعته في الهواء. وهذا يؤدي إلى انكسار شعاع الضوء عند دخوله الوسط (الزجاج) بزوايا انكسار مختلفة، فيكون انكسار الضوء الأحمر أصغر من انكسار اللون الأزرق فينفصلا عن بعضهما (أنظر الشكل)، ويخرج الشعاعان الأحمر والأزرق من الموشور منفصلين. وحيث أن الضوء الأبيض مثل ضوء الشمس يحتوي على مجموعة من الألوان تشمل تحت الحمراء والحمراء والأصفر والأخضر بدرجاته والأزرق السماوي والأزرق بدرجاته إلى الأشعة البنفسجية وفوق البنفسجية، فأن جميع تلك الألوان الضوئية تنفصل عن بعضها البعض بفعل الموشور، لاختلاف معامل انكسار كل لون في الموشور، ونحصل على ما يسمى الطيف الضوئي.

يستخدم الموشور في عملية تحليل الضوء إلى ألوان الطيف (ألوان قوس قزح)، ونظراً لأن كل عنصر من العناصر الكيميائية له طيف ضوئي خاص به، مثل بصمة الإصبع بالنسبة للإنسان، ينبعث هذا الطيف الضوئي من العنصر عند إثارة ذراته بالحرارة العالية مثلا، يظهر بعد تحليله خلف الموشور على هيئة خطوط ضوئية متوازية، فيمكن عن طريق ذلك التعرف على العنصر.

معامل الانكسار

بفرض الموشور متماثل (على الأقل مثلث متساوي الساقين أو مثلث متساوي الأضلاع) وأن الشعاع الذي يحقق زاوية أقل انحراف δ {\displaystyle \delta } يمر داخل الموشور موازياً لقاعدته ورأسه الزاوية σ {\displaystyle \sigma } ، يمكن اشتقاق العلاقة بدلالة معامل انكسار كل من الموشور n p r i s m {\displaystyle n_{prism}} والوسط خارج الموشور (عادة الهواء) n 0 {\displaystyle n_{0}} .

n p r i s m n 0 = s i n ( σ + δ 2 ) s i n ( σ 2 ) {\displaystyle {\frac {n_{prism}}{n_{0}}}={\frac {sin({\frac {\sigma +\delta }{2}})}{sin({\frac {\sigma }{2}})}}}

لإثبات ذلك سنفرض الموشور الموجود بالرسم المقابل. من الرسم نجد أن الشعاع الضوئي يسقط من D إلى A بزاوية α {\displaystyle \alpha } ومن ثم ينكسر داخل المنشور مكوناً زاوية الانكسار β {\displaystyle \beta } وعليه يتحقق قانون الانكسار:

n p r i s m n 0 = s i n α s i n β {\displaystyle {\frac {n_{prism}}{n_{0}}}={\frac {sin\alpha }{sin\beta }}}

يمكن أيضا إثبات أن زاوية الانكسار β {\displaystyle \beta } تشكل نصف زاوية رأس المنشور σ {\displaystyle \sigma } في المثلث متساو الساقين. أحد الطرق لإثبات الأمر تكمن في تماثل زوايا المثلث وبإسقاط عمود من رأسه والذي بدوره ينصف زاوية الرأس نكون قد صنعنا مثلثا قائم الزاوية، يقطع امتداد الزاوية المنكسرة β {\displaystyle \beta } . الطريقة الأخرى تكمن في أن امتداد الزاويتين المنكسرتين سيشكل مع زاوية الرأس شكل رباعي دائري (لاحتوائه زاويتين متقابلتين قامتين هما العمودان الملونان بالأخضر). بالتالي يمكن كتابة العلاقة السابقة بالصورة:

n p r i s m n 0 = s i n α s i n σ 2 {\displaystyle {\frac {n_{prism}}{n_{0}}}={\frac {sin\alpha }{sin{\frac {\sigma }{2}}}}}

مرة أخرى يكمل الشعاع المنكسر طريقه داخل الموشور موازيا للقاعدة ويخرج من الجانب الآخر عند النقطة B وينكسر مرة أخرى ماراً بالنقطة C. نظراً لتماثل المنشور، يمكننا تخيل العلاقة بشكل عكسي وإثبات زاوية انكساره عند الخروج هي أيضاً α {\displaystyle \alpha } بينما كانت قبل الخروج β {\displaystyle \beta } شريطة أن معامل انكسار الوسط على الجانب الآخر هو نفسه معامل الانكسار على الطرف السابق قبل الدخول (أي أن الوسط خارج الموشور ثابت). لاحظ أيضاً أن:

θ = α − β = α − σ 2 {\displaystyle \theta =\alpha -\beta =\alpha -{\frac {\sigma }{2}}}

وأن:

δ = θ + ( α − β ) = α − σ 2 + α − σ 2 {\displaystyle \delta =\theta +(\alpha -\beta )=\alpha -{\frac {\sigma }{2}}+\alpha -{\frac {\sigma }{2}}}

أي أن:

δ = 2 α − σ {\displaystyle \delta =2\alpha -\sigma }

أو بعبارة أخرى

α = δ + σ 2 {\displaystyle \alpha ={\frac {\delta +\sigma }{2}}}

بتعويض هذه القيمة في قانون الانكسار مرة أخرى نجد أن:

n p r i s m n 0 = s i n ( σ + δ 2 ) s i n ( σ 2 ) {\displaystyle {\frac {n_{prism}}{n_{0}}}={\frac {sin({\frac {\sigma +\delta }{2}})}{sin({\frac {\sigma }{2}})}}}

ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ

موشور مشتت

الموشور أو المنشور (بالإنجليزية: Dispersive prism)‏: في علم البصريات، أو أحد أنواع المواشير البصرية، له عادة شكل الموشور المثلثي الفراغي.

وهو النوع الأكثر شهرة من الموشورات البصرية، بالرغم من أنه قد لايكون الأكثر استخدامًا. يستخدم الموشور المثلثي لتشتيت الضوء، بحيث يتحلل إلى عناصره الطيفية. يحدث هذا التشتيت بسبب تعلق زاوية الانكسار بمعامل الانكسار، والذي بدوره يتعلق بطول الموجة. ويستخدم الموشور أيضًا لقياس معامل الانكسار لمادة الموشور وبدقة تامة.

قانون لحساب زاوية الانحراف في المنشور الثلاثي
زاوية الانحراف ح = هـ1 +خ ـ أ
حيث : ح= زاوية الانحراف ، هـ1 = زاوية السقوط ، أ= زاوية رأس المنشور
زاوية رأس المنشور أ = هـ 2 + هـ 3
هـ2= زاوية الانكسار عند الوجه الأول ، هـ3= زاوية السقوط عند الوجه الثاني