
في التصوير الفوتوغرافي ، زاوية الرؤية (AOV ) يصف المدى الزاوي لمشهد معين تم تصويره بواسطة كاميرا . يتم استخدامه بالتبادل مع المصطلح الأكثر عمومية مجال الرؤية
من المهم التمييز بين زاوية الرؤية من زاوية التغطية ، والتي تصف نطاق الزاوية الذي يمكن للعدسة تصويره. عادةً ما تكون دائرة الصورة التي تنتجها العدسة كبيرة بما يكفي لتغطية الفيلم أو المستشعر تمامًا ، وربما تتضمن بعض التظليل باتجاه الحافة. إذا كانت زاوية تغطية العدسة لا تملأ المستشعر ، فستكون دائرة الصورة مرئية ، عادةً مع تظليل قوي باتجاه الحافة ، وستقتصر زاوية الرؤية الفعالة على زاوية التغطية.
في عام 1916 ، أظهر Northey كيفية حساب زاوية الرؤية باستخدام أدوات النجارة العادية. الزاوية التي يسميها كزاوية الرؤية هي نصف الزاوية أو “الزاوية التي سيأخذها الخط المستقيم من أقصى خارج مجال الرؤية إلى مركز العدسة” ؛ ويلاحظ أن مصنعي العدسات يستخدمون ضعف هذه الزاوية.
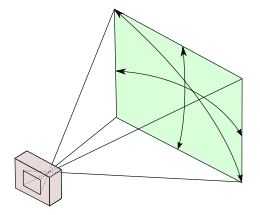
في هذه المحاكاة ، يؤدي ضبط زاوية الرؤية ومسافة الكاميرا مع الاحتفاظ بالكائن في الإطار إلى صور مختلفة اختلافًا كبيرًا. في المسافات التي تقترب من اللانهاية ، تكون أشعة الضوء متوازية تقريبًا مع بعضها البعض ، مما ينتج عنه صورة “مسطحة”. في المسافات المنخفضة وزوايا الرؤية العالية تظهر الأشياء “مختصرة”.
لا تعتمد زاوية رؤية الكاميرا على العدسة فحسب ، بل تعتمد أيضًا على المستشعر. عادة ما تكون المستشعرات الرقمية أصغر من فيلم 35 مم ، وهذا يتسبب في أن يكون للعدسة زاوية رؤية أضيق من تلك الموجودة في فيلم 35 مم ، بعامل ثابت لكل مستشعر (يسمى عامل القص ). في الكاميرات الرقمية اليومية ، يمكن أن يتراوح عامل الاقتصاص من حوالي 1 (احترافي كاميرات SLR رقمية ) ، إلى 1.6 (SLR للمستهلك) ، إلى 2 (Micro Four Thirds ILC) إلى 6 (معظم الكاميرات المدمجة ). لذا فإن العدسة القياسية مقاس 50 مم للتصوير الفوتوغرافي مقاس 35 مم تعمل كعدسة “فيلم” قياسية مقاس 50 مم على كاميرا SLR رقمية احترافية ، ولكنها تعمل بشكل أقرب إلى عدسة مقاس 80 مم (1.6 × 50 مم) في العديد من كاميرات DSLR متوسطة السوق ، وكاميرا 40 تعادل زاوية الرؤية لعدسة قياسية مقاس 50 مم على كاميرا فيلم عدسة 80 مم في العديد من كاميرات SLR الرقمية.
حساب زاوية رؤية الكاميرا
لعرض العدسات مستقيمة (غير – الصور المشوهة مكانيًا) للأجسام البعيدة ، والبعد البؤري الفعال وأبعاد تنسيق الصورة تحدد تمامًا زاوية الرؤية. تعتبر حسابات العدسات التي تنتج صورًا غير مستقيمة أكثر تعقيدًا وفي النهاية ليست مفيدة جدًا في معظم التطبيقات العملية. (في حالة العدسة ذات التشوه ، على سبيل المثال ، عدسة عين السمكة ، يمكن أن يكون للعدسة الأطول ذات التشوه زاوية رؤية أوسع من العدسة الأقصر ذات التشوه المنخفض) يمكن قياس زاوية الرؤية أفقيًا ( من الحافة اليسرى إلى اليمنى للإطار) ، عموديًا (من أعلى الإطار إلى أسفله) ، أو قطريًا (من أحد أركان الإطار إلى الزاوية المقابلة له).
بالنسبة للعدسة التي تعرض صورة مستقيمة (مركزة على اللانهاية ، انظر اشتقاق ) ، يمكن حساب زاوية الرؤية (α) من البعد المختار (د) ، والبعد البؤري الفعال (و) كالتالي:
α = 2 arctan d 2 f {\ displaystyle \ alpha = 2 \ arctan {\ frac {d} {2f}}} \ alpha = 2 \ arctan {\ frac { د} {2f}} d {\ displaystyle d} d حجم الفيلم (أو المستشعر) في الاتجاه المقاس (انظر أدناه: تأثيرات المستشعر ). على سبيل المثال ، بالنسبة للفيلم مقاس 35 مم الذي يبلغ عرضه 36 مم وارتفاعه 24 مم ، سيتم استخدام d = 36 {\ displaystyle d = 36} d = 36 mm للحصول على زاوية الرؤية الأفقية و د = 24 {\ displaystyle d = 24} d = 24 ملم للزاوية الرأسية.
نظرًا لأن هذه دالة مثلثية ، فإن زاوية الرؤية لا تتغير بشكل خطي تمامًا مع مقلوب الطول البؤري. ومع ذلك ، باستثناء العدسات ذات الزاوية العريضة ، من المعقول تقريب α ≈ df {\ displaystyle \ alpha \ almost {\ frac {d} {f}}} \ alpha \ almost {\ frac {d} {f} } راديان أو 180 د π و {\ displaystyle {\ frac {180d} {\ pi f}}} {\ frac {180d} {\ pi f}} درجة.
الطول البؤري الفعال يساوي تقريبًا الطول البؤري المحدد للعدسة (F) ، باستثناء تصوير الماكرو حيث تكون مسافة العدسة إلى الجسم قابلة للمقارنة مع البعد البؤري. في هذه الحالة ، يجب مراعاة عامل التكبير (م):
f = F ⋅ (1 + m) {\ displaystyle f = F \ cdot (1 + m)} f = F \ cdot (1 + m) (في التصوير الفوتوغرافي m {\ displaystyle m} م عادةً ما يتم تعريفه على أنه موجب ، على الرغم من الصورة المقلوبة.) على سبيل المثال ، مع نسبة تكبير 1: 2 ، نجد f = 1.5 ⋅ فهرنهايت {\ displaystyle f = 1.5 \ cdot F} f = 1.5 \ cdot F وبالتالي يتم تقليل زاوية الرؤية بنسبة 33٪ مقارنة بالتركيز على كائن بعيد بنفس العدسة.
يمكن أيضًا تحديد زاوية الرؤية باستخدام جداول FOV أو الآلات الحاسبة للعدسات الورقية أو البرمجية.
الرسوم البيانية لوغاريتم تسجيل الطول البؤري مقابل عامل الاقتصاص مقابل زوايا الرؤية القطرية والأفقية والعمودية للفيلم أو مستشعرات نسب العرض إلى الارتفاع 3: 2 و 4: 3. يُظهر الخط الأصفر مثالاً حيث يساوي 18 مم في 3: 2 APS-C 27 مم وينتج زاوية عمودية قدرها 48 درجة.
مثال
ضع في اعتبارك كاميرا مقاس 50 مم بها عدسة بها الطول البؤري F = 50 مم. تبلغ أبعاد تنسيق الصورة 35 مم 24 مم (رأسيًا) × 36 مم (أفقيًا) ، مما يعطي قطرًا يبلغ حوالي 43.3 مم.
عند التركيز اللانهائي ، f = F ، زوايا الرؤية هي:
أفقيًا ، α h = 2 arctan h 2 f = 2 arctan 36 2 × 50 ≈ 39.6 ∘ {\ displaystyle \ alpha _ {h} = 2 \ arctan {\ frac {h} {2f}} = 2 \ arctan {\ frac {36} {2 \ times 50}} \ almost 39.6 ^ {\ circ}} \ alpha _ {h} = 2 \ arctan {\ frac {h} {2f}} = 2 \ arctan {\ frac {36} {2 \ t imes 50}} \ حوالي 39.6 ^ {\ circ}
عموديًا ، α v = 2 arctan v 2 f = 2 arctan 24 2 × 50 ≈ 27.0 ∘ {\ displaystyle \ alpha _ {v} = 2 \ arctan {\ frac {v} {2f}} = 2 \ arctan {\ frac {24} {2 \ times 50}} \ حوالي 27.0 ^ {\ circ}} \ alpha _ {v} = 2 \ arctan {\ frac { v} {2f}} = 2 \ arctan {\ frac {24} {2 \ times 50}} \ حوالي 27.0 ^ {\ circ}
قطريًا ، α d = 2 arctan d 2 f = 2 arctan 43.3 2 × 50 ≈ 46.8 ∘ {\ displaystyle \ alpha _ {d} = 2 \ arctan {\ frac {d} {2f}} = 2 \ arctan {\ frac {43.3} {2 \ times 50}} \ almost 46.8 ^ {\ circ} } \ alpha _ {d} = 2 \ arctan {\ frac {d} {2f}} = 2 \ arctan {\ frac {43.3} {2 \ times 50}} \ حوالي 46.8 ^ {\ circ } اشتقاق صيغة زاوية الرؤية
ضع في اعتبارك عدسة مستقيمة في الكاميرا تُستخدم لتصوير كائن على مسافة S 1 {\ displaystyle S_ {1}} S_ {1} ، وتشكيل صورة بالكاد تتناسب مع البعد ، د {displaystyle d} d ، من الإطار (فيلم أو مستشعر الصورة ). تعامل مع العدسة كما لو كانت ثقبًا صغيرًا على مسافة S 2 {\ displaystyle S_ {2}} S_ {2} من مستوى الصورة (من الناحية الفنية ، مركز منظور العدسة المستقيمة في وسط بؤبؤ العين ):
زاوية رؤية العدسة. svg
الآن α / 2 {\ displaystyle \ alpha / 2} \ alpha / 2 هي الزاوية بين المحور البصري للعدسة والشعاع يربط مركزها البصري بحافة الفيلم. هنا يتم تعريف α {\ displaystyle \ alpha} \ alpha على أنه زاوية الرؤية ، نظرًا لأنها الزاوية التي تحتوي على أكبر جسم يمكن أن تتناسب صورته مع الفيلم. نريد إيجاد العلاقة بين:
الزاوية α {\ displaystyle \ alpha} \ alpha
الجانب "المعاكس" من المثلث الأيمن ، د / 2 {\ displaystyle d / 2} d / 2 (نصف أبعاد تنسيق الفيلم)
الجانب "المجاور" ، S 2 {\ displaystyle S_ {2}} S_ {2} (المسافة من العدسة إلى مستوى الصورة) باستخدام حساب المثلثات الأساسي ، نجد:
tan (α / 2) = d / 2 S 2. {\ displaystyle tan (alpha / 2) = { \ frac {d / 2} {S_ {2}}}.} \ tan ( \ alpha / 2) = {\ frac {d / 2} {S_ {2}}}. يمكننا حلها من أجل α ، مع إعطاء:
α = 2 arctan d 2 S 2 {\ displaystyle \ alpha = 2 \ arctan { \ frac {d} {2S_ {2}}}} \ alpha = 2 \ arctan {\ frac {d} {2S_ {2}}} لعرض صورة واضحة لكائنات بعيدة ، يجب أن يكون S 2 {\ displaystyle S_ {2}} S_ {2} مساويًا لـ البعد البؤري ، F {\ displaystyle F} ف ، والذي يتم الوصول إليه عن طريق ضبط العدسة على تركيز اللانهاية . ثم يتم إعطاء زاوية الرؤية من خلال:
α = 2 arctan d 2 f {\ displaystyle \ alpha = 2 \ arctan {\ frac {d} {2f}}} \ alpha = 2 \ arctan {\ frac { د} {2f}} حيث f = F {\ displaystyle f = F} f = F لاحظ أن زاوية الرؤية تختلف قليلاً عندما لا يكون التركيز على اللانهاية (انظر التنفس (العدسة) ) ، معطى بواسطة S 2 = S 1 f S 1 – f {\ displaystyle S_ {2} = {\ frac {S_ {1} f} {S_ {1} -f}}} S_ {2} = {\ frac {S_ {1} و} {S_ {1} -f}} إعادة ترتيب معادلة العدسة.
تصوير الماكرو
لتصوير الماكرو ، لا يمكننا إهمال الفرق بين S 2 {\ displaystyle S_ {2}} S_ {2} و F {\ displaystyle F} ف . من صيغة العدسة الرقيقة ,
1 F = 1 S 1 + 1 S 2 {\ displaystyle {\ frac {1} {F}} = {\ frac {1} {S_ {1}}} + { \ frac {1} {S_ {2}}}} {\ frac {1} {F}} = {\ frac {1} {S_ {1}}} + {\ frac {1} {S_ {2}}} .من تعريف التكبير ، m = S 2 / S 1 {\ displaystyle m = S_ {2} / S_ { 1}} m = S_ {2} / S_ {1} ، يمكننا استبدال S 1 {\ displaystyle S_ {1}} S_ {1} ومع بعض الجبر أوجد:
S 2 = F ⋅ (1 + m ) {\ displaystyle S_ {2} = F \ cdot (1 + m)} S_ {2} = F \ cdot (1 + m) تعريف f = S 2 {\ displaystyle f = S_ {2}} f = S_ {2} باعتباره “البؤرة الفعالة length “، نحصل على الصيغة المعروضة أعلاه:
α = 2 arctan d 2 f {\ displaystyle \ alpha = 2 \ arctan {\ frac {d} {2f}}} \ alpha = 2 \ arctan {\ frac { د} {2f}} حيث f = F ⋅ (1 + m) {\ displaystyle f = F \ cdot (1 + m)} f = F \ cdot (1 + m) .التأثير الثاني الذي يلعب دوره في التصوير الفوتوغرافي المقرب هو عدم تناسق العدسة (العدسة غير المتماثلة هي العدسة حيث تكون الفتحة يبدو أن لها أبعادًا مختلفة عند عرضها من الأمام ومن الخلف). يتسبب عدم تناسق العدسة في حدوث إزاحة بين المستوى العقدي ومواقع التلميذ. يمكن قياس التأثير باستخدام النسبة (P) بين قطر خروج التلميذ الظاهر وقطر بؤبؤ العين. تصبح الصيغة الكاملة لزاوية الرؤية الآن:
α = 2 arctan d 2 F ⋅ (1 + m / P) {\ displaystyle \ alpha = 2 \ arctan {\ frac {d} {2F \ cdot (1 + m / P)}} \ alpha = 2 \ arctan {\ frac {d} {2F \ cdot (1 + m / P)}} قياس مجال رؤية الكاميرا
رسم تخطيطي لجهاز بصري ميزاء يستخدم في قياس مجال الرؤية للكاميرا.
في صناعة الأجهزة البصرية غالبًا ما يستخدم مصطلح مجال الرؤية (FOV) ، على الرغم من أن القياسات لا يزال يتم التعبير عنها كزوايا. تُستخدم الاختبارات البصرية بشكل شائع لقياس مجال الرؤية UV, المرئي و الأشعة تحت الحمراء (الأطوال الموجية حوالي 0.1-20 ميكرومتر في الطيف الكهرومغناطيسي ) أجهزة الاستشعار والكاميرات.
الغرض من هذا الاختبار هو قياس مجال الرؤية الأفقي والرأسي للعدسة والمستشعر المستخدم في نظام التصوير ، عندما يكون البعد البؤري للعدسة أو حجم المستشعر غير معروف (أي عندما يكون الحساب أعلاه لا ينطبق على الفور). على الرغم من أن هذه طريقة نموذجية تستخدمها صناعة البصريات لقياس مجال الرؤية ، إلا أن هناك العديد من الطرق الممكنة الأخرى.
الأشعة فوق البنفسجية / الضوء المرئي من مجال متكامل (و / أو مصدر آخر مثل جسم أسود ) يركز على هدف اختبار مربع في المستوى البؤري من ميزاء (المرايا في الرسم التخطيطي) ، بحيث يمكن رؤية صورة افتراضية لهدف الاختبار بعيدًا بلا حدود بواسطة الكاميرا قيد الاختبار. تستشعر الكاميرا قيد الاختبار صورة حقيقية للصورة الافتراضية للهدف ، ويتم عرض الصورة المحسوسة على شاشة.
شاشة عرض الصورة المحسوسة من الكاميرا قيد الاختبار
الصورة المحسوسة ، والتي تتضمن الهدف ، على الشاشة ، حيث يمكن قياسها. يتم تحديد أبعاد عرض الصورة الكاملة وجزء الصورة الهدف عن طريق الفحص (عادةً ما تكون القياسات بالبكسل ، ولكن يمكن أيضًا أن تكون بالبوصة أو السنتيمتر).
D {\ displaystyle D} D = أبعاد الصورة الكاملة
د {\ displaystyle d} d = أبعاد صورة الهدف الصورة الافتراضية البعيدة للميزاء الهدف يقابل زاوية معينة ، يشار إليها باسم المدى الزاوي للهدف ، والتي تعتمد على الطول البؤري الموازاة وحجم الهدف. بافتراض أن الصورة المحسوسة تتضمن الهدف بالكامل ، فإن الزاوية التي تراها الكاميرا ، مجال الرؤية الخاص بها ، هي هذا المدى الزاوي للهدف مضروبًا في نسبة حجم الصورة الكامل إلى حجم الصورة المستهدفة.
المدى الزاوي للهدف هو:
α = 2 arctan L 2 fc {\ displaystyle \ alpha = 2 \ arctan {\ frac {L} {2f_ {c}}}} \ alpha = 2 \ arctan {\ frac {L} {2f_ {c}}}
حيث L {\ displaystyle L} L هو بُعد الهدف و fc {\ displaystyle f_ {c}} f_ {c} هو الطول البؤري للميزاء. يكون مجال الرؤية الكلي عندئذٍ تقريبًا:
FOV = α D d {\ displaystyle \ mathrm {FOV} = \ alpha {\ frac {D} {d}}} \ mathrm {FOV} = \ alpha {\ frac {D} {d}} أو بشكل أكثر دقة ، إذا كان نظام التصوير مستقيمًا :
FOV = 2 arctan LD 2 fcd {\ displaystyle \ mathrm {FOV} = 2 \ arctan {\ frac {LD} {2f_ {c} d}}} \ mathrm {FOV} = 2 \ arctan {\ frac {LD} {2f_ {c} d}} يمكن أن يكون هذا الحساب أفقيًا أو رأسيًا مجال الرؤية ، اعتمادًا على كيفية الهدف والصورة تقاس.
أنواع العدسات وتأثيراتها
الطول البؤري
كيف يؤثر الطول البؤري على المنظور: تغيير الأطوال البؤرية عند نفس حجم المجال الذي تحققه كاميرا مختلفة – مسافات موضوعية. لاحظ أنه كلما كان الطول البؤري أقصر وزاوية الرؤية أكبر ، كلما زاد تشوه المنظور وازدادت الاختلافات في الحجم.
غالبًا ما يشار إلى العدسات بمصطلحات تعبر عن زاوية الرؤية:
عدسات عين السمكة ، تتراوح الأطوال البؤرية النموذجية بين 8 مم و 10 مم للصور الدائرية ، و15-16 مم للصور ذات الإطار الكامل. حتى 180 درجة وما بعدها.
A عدسة عين السمكة الدائرية (على عكس عدسة عين السمكة ذات الإطار الكامل) هي مثال على العدسة حيث تكون زاوية التغطية أقل من زاوية الرؤية. الصورة المسقطة على الفيلم دائرية لأن قطر الصورة المسقطة أضيق من ذلك المطلوب لتغطية الجزء الأوسع من الفيلم.
عدسة الزاوية فائقة الاتساع هي مستقيمة وهي أقل من 24 مم من طول بؤري في تنسيق فيلم 35 مم ، هنا يعطي 14 مم 114 درجة و 24 مم يعطي 84 درجة.
عدسات بزاوية عريضة (24-35 مم في 35 مم فيلم) يغطي ما بين 84 درجة و 64 درجة
عدسات عادية أو قياسية (36-60 مم بصيغة فيلم 35 مم) تغطي ما بين 62 درجة و 40 درجة
عدسات ذات تركيز طويل (أي العدسة ذات البعد البؤري الأكبر من القطر للفيلم أو المستشعر المستخدم) يكون لها عمومًا زاوية رؤية 35 درجة أو أقل. نظرًا لأن المصورين عادةً ما يصادفون فقط النوع الفرعي من العدسة المقربة ، يشار إليهم في لغة التصوير الشائعة على النحو التالي:
"تقريب متوسط" ، وهو طول بؤري من 85 مم إلى 250 مم في 35 تنسيق فيلم مم يغطي ما بين 30 درجة و 10 درجات
"تليفوتوغرافي فائق" (أكثر من 300 مم في تنسيق فيلم 35 مم) يغطي بشكل عام ما بين 8 درجات إلى أقل من 1 درجة عدسات تكبير هي حالة خاصة حيث يمكن تغيير البعد البؤري ، وبالتالي زاوية الرؤية ، للعدسة ميكانيكيًا دون إزالة العدسة من الكاميرا.
الخصائص
بالنسبة لكاميرا معينة – مسافة الهدف ، تعمل العدسات الأطول على تكبير الموضوع بشكل أكبر. لتكبير موضوع معين (وبالتالي مسافات مختلفة بين الكاميرا والهدف) ، يبدو أن العدسات الأطول تضغط على المسافة ؛ تظهر العدسات الأوسع لتوسيع المسافة بين الكائنات.
نتيجة أخرى لاستخدام عدسة بزاوية عريضة تتمثل في تشوه منظور واضح بدرجة أكبر عندما لا تكون الكاميرا محاذاة بشكل عمودي مع الموضوع: تتلاقى الخطوط المتوازية بنفس معدل عدسة عادية ، ولكن تتقارب بشكل أكبر بسبب المجال الكلي الأوسع. على سبيل المثال ، يبدو أن المباني تتساقط للخلف بشكل أكثر شدة عندما يتم توجيه الكاميرا لأعلى من مستوى الأرض أكثر مما لو تم تصويرها بعدسة عادية على نفس المسافة من الهدف ، لأن المزيد من مبنى الهدف مرئي على نطاق واسع- لقطة زاوية.
نظرًا لأن العدسات المختلفة تتطلب عمومًا مسافة مختلفة بين الكاميرا والهدف للحفاظ على حجم الهدف ، فإن تغيير زاوية الرؤية يمكن أن يؤدي بشكل غير مباشر إلى تشويه المنظور ، وتغيير الحجم النسبي الظاهر للهدف و المقدمة.
إذا ظل حجم صورة الهدف كما هو ، فعند أي فتحة معينة ، ستعطي جميع العدسات والزاوية الواسعة والعدسات الطويلة نفس عمق المجال .
مثال على كيفية تأثير اختيار العدسة على زاوية الرؤية.
عدسة 28 مم ، عدسة 65.5 ° × 46.4 °
50 مم ، 39.6 ° × 27.0 °
عدسة 70 مم ، 28.9 ° × 19.5 °
210 مم عدسة ، 9.8 ° × 6.5 °
زوايا رؤية العدسة الشائعة
يوضح هذا الجدول زوايا الرؤية القطرية والأفقية والعمودية ، بالدرجات ، للعدسات التي تنتج صورًا مستقيمة ، عند استخدامها بصيغة 36 مم × 24 مم (أي 135 فيلم أو إطار كامل 35 مم رقمي باستخدام العرض 36 مم ، الارتفاع 24 مم ، وقطري 43.3 مم لـ d في الصيغة أعلاه). تشير الكاميرات الرقمية المدمجة أحيانًا إلى الأطوال البؤرية لعدساتها بمكافئ 35 مم ، والتي يمكن استخدامها في هذا الجدول.
للمقارنة ، يرى النظام البصري البشري زاوية رؤية تبلغ حوالي 140 درجة × 80 درجة.
الطول البؤري (مم) قطري (درجة) عمودي (°) أفقي (°)
0 180.0 180.0 180.0
2 169.4 161.1 166.9
12 122.0 90.0 111.1
14 114.2 81.2 102.7
16 107.1 73.9 95.1
20 94.5 61.9 82.4
24 84.1 53.1 73.7
35 63.4 37.8 54.4
50 46.8 27.0 39.6
70 34.4 19.5 28.8
85 28.6 16.1 23.9
105 23.3 13.0 19.5
200 12.3 6.87 10.3
300 8.25 4.58 6.87
400 6.19 3.44 5.15
500 4.96 2.75 4.12
600 4.13 2.29 3.44
700 3.54 1.96 2.95
800 3.10 1.72 2.58
1200 2.07 1.15 1.72
خمس صور باستخدام 24 و 28 و 35 و 50 و 72 أطوال تكبير مكافئة مم ، تنسيق عمودي ، لتوضيح زوايا الرؤية
خمس صور باستخدام وظيفة تكبير خطوة مكافئة 24 و 28 و 35 و 50 و 72 مم ، لتوضيح زوايا الرؤية
تأثيرات حجم المستشعر (“عامل الاقتصاص” )
كما هو مذكور أعلاه ، لا تعتمد زاوية رؤية الكاميرا على العدسة فحسب ، بل تعتمد أيضًا على المستشعر المستخدم. عادةً ما تكون المستشعرات الرقمية أصغر من فيلم 35 مم ، مما يتسبب في أن تتصرف العدسة عادةً كعدسة ذات طول بؤري أطول ، ولها زاوية رؤية أضيق من فيلم 35 مم ، بواسطة عامل ثابت لكل مستشعر (يسمى <86)>عامل المحاصيل ). في الكاميرات الرقمية اليومية ، يمكن أن يتراوح عامل الاقتصاص من حوالي 1 (احترافي كاميرات SLR رقمية ) ، إلى 1.6 (كاميرات SLR متوسطة السوق) ، إلى حوالي 3 إلى 6 للكاميرات المدمجة . لذا ، فإن العدسة القياسية مقاس 50 مم تعمل مثل عدسة “فيلم” قياسية مقاس 50 مم حتى على كاميرا SLR رقمية احترافية ، ولكنها ستعمل بالقرب من عدسة مقاس 75 مم (1.5 × 50 مم نيكون) أو عدسة مقاس 80 مم (مقاس 1.6 × 50 مم من Canon) على العديد من DSLRs متوسطة السوق ، وزاوية الرؤية 40 درجة لعدسة قياسية مقاس 50 مم على كاميرا فيلم تعادل عدسة مقاس 28-35 مم على العديد من كاميرات SLR الرقمية.
يوضح الجدول أدناه زوايا الرؤية الأفقية والعمودية والقطرية ، بالدرجات ، عند استخدامها بتنسيق 22.2 مم × 14.8 مم (أي حجم إطار Canon DSLR APS-C ) و قطري 26.7 مم.
الطول البؤري (مم) القطر (°) الرأسي (°) الأفقي (°)
2 162.9 149.8 159.6
4 146.6 123.2 140.4
7 124.6 93.2 115.5
9 112.0 78.9 101.9
12 96.1 63.3 85.5
14 87.2 55.7 76.8
16 79.6 49.6 69.5
17 76.2 47.0 66.3
18 73.1 44.7 63.3
20 67.4 40.6 58.1
24 58.1 34.3 49.6
35 41.7 23.9 35.2
50 29.9 16.8 25.0
70 21.6 12.1 18.0
85 17.8 10.0 14.9
105 14.5 8.1 12.1
200 7.6 4.2 6.4
210 7.3 4.0 6.1
300 5.1 2.8 4.2
400 3.8 2.1 3.2
500 3.1 1.7 2.5
600 2.5 1.4 2.1
700 2.2 1.2 1.8
800 1.9 1.1 1.6
التصوير السينمائي وألعاب الفيديو
النسبة دقة 1080 بكسل الاسم الشائع تنسيق / عدسة الفيديو
32:27 1280x1080p DVCPRO HD
4: 3 1440x1080p
16: 9 1920x1080p شاشة عريضة
2: 1 2160×1080 18: 9 Univisium
64:27 2560x1080p Ultra-Widescreen Cinemascope / Anamorphic
32: 9 3840x1080p Super Ultra-Widescreen Ultra-Widescreen 3.6 / Anamorphic 3.6
تعديل زاوية العرض بمرور الوقت (المعروف باسم التكبير ) ، هو أسلوب سينمائي مستخدم بشكل متكرر ، وغالبًا ما يتم دمجه مع حركة الكاميرا لإنتاج تأثير “زوم دوللي ” ، اشتهر بواسطة فيلم دوار . يمكن أن يؤدي استخدام زاوية رؤية واسعة إلى المبالغة في سرعة الكاميرا المتصورة ، وهو أسلوب شائع في لقطات تتبع و جولات فانتوم و ألعاب فيديو سباقات . راجع أيضًا مجال الرؤية في ألعاب الفيديوWikipedia site:ar.wikichi.ru

