مجلة فن التصوير

fotoartbook

التراث اللامادي موسوعة فن التصوير

تعرفوا ما هو #البعد_ البؤري أو #الطول_ البؤري أو# المسافة_ البؤرية Focal length‏ المسافة بين المركز البصري للعدسة ونقطة تجمّع الأشعة المنكسرة.

من فريد ظفور

بعد بؤري
من ويكيبيديا
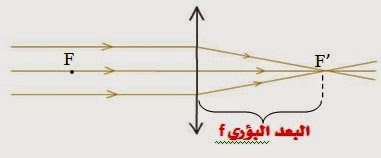
البعد البؤري أو الطول البؤري أو المسافة البؤرية (بالإنجليزية: Focal length)‏ المسافة بين المركز البصري للعدسة (أو قطب المرآة) ونقطة تجمّع الأشعة المنكسرة(أو المنعكسة)أو امتدادتها على المحور الرئيسي. والبعد البؤرى يساوى نصف القطر للجسم العاكس وتفيد هذه الخاصية في الاطباق العاكسة الخاصة بالاقمار الاصطناعيه . ان مجموع مقلوبي بُعد الصورة وبُعد الجسم يساوي مقلوب البعد البؤري.


كاميرا Minox LX بنقطة حمراء فائقة البؤرة
المسافة البؤرية – Hyperfocal distance
في بصريات و التصوير, مسافة فائقة البؤرة هي المسافة التي يمكن بعدها وضع جميع الأشياء في “مقبول” التركيز. نظرًا لأن مسافة التركيز البؤري هي مسافة التركيز التي تعطي الحد الأقصى عمق الميدان، إنها المسافة المرغوبة لتعيين التركيز على كاميرا ذات تركيز ثابت.[1] تعتمد المسافة البؤرية بشكل كامل على مستوى الحدة الذي يعتبر مقبولاً.
تتميز المسافة البؤرية بخاصية تسمى “أعماق المجال المتتالية” ، حيث تركز العدسة على جسم تكون بعده على مسافة فائقة البؤرة ح سيعمل على عمق المجال من ح/ 2 إلى ما لا نهاية ، إذا تم التركيز على العدسة ح/ 2 ، سوف يمتد عمق المجال من ح/ 3 إلى ح؛ إذا تم التركيز بعد ذلك على العدسة ح/ 3 ، سوف يمتد عمق المجال من ح/ 4 إلى ح/ 2 ، إلخ.
توماس ساتون وكتب جورج داوسون لأول مرة عن المسافة البؤرية (أو “النطاق البؤري”) في عام 1867.[2] قد يكون لويس دير في عام 1906 أول من اشتق معادلة للمسافة البؤرية. رودولف كينجسليك كتب في عام 1951 عن طريقتين لقياس المسافة البؤرية.
بعض الكاميرات لها مسافة فائقة البؤرة محددة على قرص التركيز. على سبيل المثال ، على قرص التركيز Minox LX توجد نقطة حمراء بين 2 متر وما لا نهاية ؛ عندما يتم ضبط العدسة على النقطة الحمراء ، أي التركيز على المسافة البؤرية ، فإن عمق المجال يمتد من 2 متر إلى ما لا نهاية.
طريقتان:
هناك طريقتان شائعتان للتعريف والقياس مسافة فائقة البؤرة، مما يؤدي إلى قيم تختلف قليلاً فقط. نادرًا ما يتم التمييز بين المعنيين ، نظرًا لأن قيمهما متطابقة تقريبًا. القيمة المحسوبة وفقًا للتعريف الأول تتجاوز القيمة المحسوبة من الثانية بمقدار واحد فقط البعد البؤري.
التعريف 1: المسافة البؤرية هي أقرب مسافة يكون عندها a عدسة يمكن أن تركز مع الاحتفاظ كائنات في اللانهاية بشكل مقبول. عندما تكون العدسة مركزة على هذه المسافة ، فإن كل الأجسام على مسافات من نصف المسافة البؤرية إلى اللانهاية ستكون حادة بشكل مقبول.
التعريف 2: المسافة البؤرية هي المسافة التي تكون بعدها جميع الكائنات حادة بشكل مقبول ، لعدسة مركزة على اللانهاية.
الحدة المقبولة:
الصيغ:

للتعريف الأول ،H = { frac {f ^ {2}} {Nc}} + f

أينح هي المسافة البؤريةF يكون البعد البؤرين يكون رقم f (و / د لقطر الفتحة د)ج هل دائرة الارتباك حد

بالنسبة إلى أي رقم بؤري عملي ، فإن البعد البؤري المضاف غير مهم مقارنة بالمصطلح الأول ، لذلكح تقريبًا { frac {f ^ {2}} {Nc}}

هذه الصيغة دقيقة للتعريف الثاني ، إذا ح يقاس من عدسة رفيعة أو من المستوى الرئيسي الأمامي لعدسة معقدة ؛ وهو أيضًا دقيق بالنسبة للتعريف الأول إذا ح يقاس من نقطة ذات بعد بؤري واحد أمام المستوى الرئيسي الأمامي. لأغراض عملية ، لا يوجد فرق كبير بين التعريفين الأول والثاني.

الاشتقاق باستخدام البصريات الهندسية

الشخصيات المصاحبة

الاشتقاقات التالية تشير إلى الأرقام المصاحبة. من أجل الوضوح ، يشار إلى نصف الفتحة ودائرة التشويش.[3]

التعريف 1

كائن على مسافة ح يشكل صورة حادة عن بعد x (خط أزرق). هنا ، تحتوي الكائنات الموجودة في اللانهاية على صور بها دائرة من الارتباك يشير إليها الشكل البيضاوي البني حيث يتقاطع الشعاع الأحمر العلوي من خلال النقطة المحورية مع الخط الأزرق.

أولاً باستخدام مثلثات متشابهة مظللة باللون الأخضر ،{ start {array} {crcl} & { dfrac {xf} {c / 2}} & = & { dfrac {f} {D / 2}} وبالتالي & x-f & = & { dfrac { cf} {D}} وبالتالي & x & = & f + { dfrac {cf} {D}} end {array}}

ثم باستخدام مثلثات مماثلة منقطة باللون الأرجواني ،{ start {array} {crclcl} & { dfrac {H} {D / 2}} & = & { dfrac {x} {c / 2}} وبالتالي & H & = & { dfrac {Dx} {c}} & = & { dfrac {D} {c}} { Big (} f + { dfrac {cf} {D}} { Big)} && = & { dfrac {Df} { c}} + f & = & { dfrac {f ^ {2}} {Nc}} + f end {array}}على النحو الوارد أعلاه.

التعريف 2

الكائنات في اللانهاية تشكل صورًا حادة عند البعد البؤري F (خط أزرق). هنا ، كائن في ح تشكل صورة بدائرة من التشويش يشير إليها الشكل البيضاوي البني حيث يتقاطع الشعاع الأحمر السفلي مع صورته الحادة مع الخط الأزرق.

باستخدام مثلثات مماثلة مظللة باللون الأصفر ،{ begin {array} {crclcl} & { dfrac {H} {D / 2}} & = & { dfrac {f} {c / 2}} وبالتالي & H & = & { dfrac {Df} {c}} & = & { dfrac {f ^ {2}} {Nc}} end {array}}

مثال

recommended byLIMELIGHT MEDIAما تريده المرأة: 7 صفات للرجال تحتاجها كل امرأةإعرف أكثر

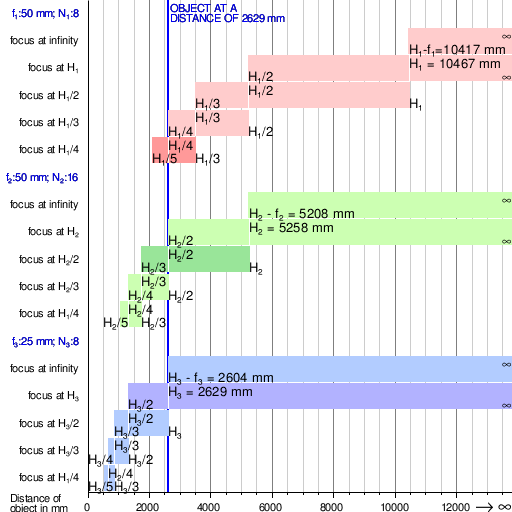
أعماق المجال من 3 مثالي العدسات من أطوال بؤرية, F1, F2 و F3و و أرقام و ن1, ن2 و ن3 عند التركيز على أشياء على مسافات مختلفة. ح1, ح2 و ح3 تشير إلى كل منهما مسافات مفرطة البؤرة (باستخدام التعريف 1 في تلك المقالة) مع دائرة الارتباك بقطر 0.03 مم. توضح الأشرطة الأكثر قتامة كيفية زيادة عمق المجال ، بالنسبة لمسافة الهدف الثابتة ، باستخدام طول بؤري أقصر أو فتحة أصغر. يوضح الشريط العلوي الثاني من كل مجموعة تكوين ملف تركيز ثابت الة تصوير مع ضبط التركيز البؤري بشكل دائم على مسافة فائقة البؤرة لزيادة عمق المجال.

على سبيل المثال ، بالنسبة لعدسة مقاس 50 مم في f / 8 باستخدام دائرة ارتباك تبلغ 0.03 مم ، وهي قيمة تستخدم عادةً في التصوير الفوتوغرافي مقاس 35 مم ، وهي المسافة البؤرية وفقًا لـ التعريف 1 يكونH = { frac {(50) ^ {2}} {(8) (0.03)}} + (50) = 10467 { mbox {mm}}

إذا كانت العدسة مركزة على مسافة 10.5 م ، فإن كل شيء من نصف تلك المسافة (5.2 م) إلى اللانهاية سيكون حادًا بشكل مقبول في صورتنا. مع صيغة التعريف 2والنتيجة هي 10417 ملم بفارق 0.5٪.

أعماق متتالية للمجال

PROMOTED CONTENT

6 Reasons Sharks Are Afraid Of DolphinsBrainberriesحسابات تيك توك هذه هي الأفضل بكل بساطةBrainberriesما الذي يخبأه ماضي ملكة الأردنHerbeautyلم يعرف أحد هذه المعلومات عن ملك الأردنBrainberries

تتميز المسافة البؤرية بخاصية غريبة: بينما تركز العدسة على ح سيعمل على عمق المجال من ح/ 2 إلى ما لا نهاية ، إذا تم التركيز على العدسة ح/ 2 ، سوف يمتد عمق المجال من ح/ 3 إلى ح؛ إذا تم التركيز بعد ذلك على العدسة ح/ 3 ، سوف يمتد عمق المجال من ح/ 4 إلى ح/ 2. يستمر هذا من خلال جميع المتتالية 1 /x قيم المسافة البؤرية.

يسمي بايبر (1901) هذه الظاهرة “أعماق الحقل المتتالية” ويوضح كيفية اختبار الفكرة بسهولة. هذا أيضًا من بين أقدم المنشورات التي استخدمت الكلمة فرط البؤرة.

يوضح الشكل الموجود على اليمين هذه الظاهرة.

التاريخ

PROMOTED CONTENT

ما تريده المرأة: 7 صفات للرجال تحتاجها كل امرأةLimelight Media6 Reasons Sharks Are Afraid Of DolphinsBrainberriesأثارت هذه الصورة ضجة كبيرة على كل مواقع التواصل الاجتماعيLimelight Mediaهذا الاستخدام المبكر للمصطلح مسافة فائقة البؤرة، Derr 1906 ، ليس بأي حال من الأحوال أقرب تفسير لهذا المفهوم.

مفاهيم التعريفيين للمسافة البؤرية لها تاريخ طويل ، مرتبطة بمصطلحات عمق المجال ، عمق التركيز ، دائرة الارتباك ، إلخ. فيما يلي بعض الاقتباسات والتفسيرات المبكرة المختارة حول الموضوع.

ساتون وداوسون 1867

يحدد توماس ساتون وجورج داوسون النطاق البؤري لما نسميه الآن مسافة فائقة البؤرة:[2]

المدى البؤري. يوجد في كل عدسة ، المقابلة لنسبة فتحة معينة (أي نسبة قطر نقطة التوقف إلى البعد البؤري) ، مسافة معينة من جسم قريب منه ، والتي تكون جميع الكائنات بينها وبين اللانهاية متساوية في الجودة التركيز. على سبيل المثال ، في عدسة عرض واحدة بتركيز 6 بوصات ، مع توقف 1/4 بوصة (نسبة الفتحة واحد وعشرون 24) ، تقع جميع الكائنات على مسافات تقع بين 20 قدمًا من العدسة ومسافة لانهائية منها ( نجمة ثابتة ، على سبيل المثال) في تركيز جيد بنفس القدر. لذلك يُطلق على عشرين قدمًا اسم “النطاق البؤري” للعدسة عند استخدام هذا التوقف. وبالتالي ، فإن النطاق البؤري هو مسافة أقرب كائن ، والذي سيكون في بؤرة جيدة عندما يتم ضبط زجاج الأرض لجسم بعيد جدًا. في نفس العدسة ، سيعتمد النطاق البؤري على حجم الحجاب الحاجز المستخدم ، بينما في العدسات المختلفة التي لها نفس نسبة الفتحة ، ستكون النطاقات البؤرية أكبر مع زيادة الطول البؤري للعدسة. “النطاق البؤري” لم يدخل حيز الاستخدام العام ، ولكن من المرغوب جدًا أن يتم ذلك ، من أجل منع الغموض والالتفاف عند معالجة خصائص عدسات التصوير. يعد “النطاق البؤري” مصطلحًا جيدًا ، لأنه يعبر عن النطاق الذي من الضروري ضمنه ضبط تركيز العدسة على الأشياء الموجودة على مسافات مختلفة عنها – وبعبارة أخرى ، النطاق الذي يصبح التركيز فيه ضروريًا.

يبلغ نطاقها البؤري حوالي 1000 ضعف قطر فتحة العدسة ، لذا فمن المنطقي أن تكون المسافة البؤرية مع قيمة CoC لـ F/ 1000 ، أو تنسيق الصورة قطري مرات 1/1000 على افتراض أن العدسة هي عدسة “عادية”. ومع ذلك ، فإن ما هو غير واضح هو ما إذا كان النطاق البؤري الذي يذكرونه محسوبًا أم تجريبيًا.

أبني 1881

يقول السير وليام دي ويفليسلي أبني:[4]

ستعطي الصيغة المرفقة أقرب نقطة تقريبًا ص والتي ستظهر في البؤرة عندما يتم التركيز بدقة على المسافة ، بافتراض أن قرص الارتباك المسموح به هو 0.025 سم:ص = 0.41 cdot f ^ {2} cdot aمتىو = البعد البؤري للعدسة في سمأ = نسبة الفتحة إلى البعد البؤري

هذا هو، أ هو المقابل لما نسميه الآن F-عدد والجواب واضح بالمتر. من الواضح أن 0.41 له سيكون 0.40. بناءً على صيغه ، وعلى فكرة أن ملف نسبة الفتحة يقول أبني: يجب أن تظل ثابتة في المقارنات عبر التنسيقات:

يمكن إثبات أن التكبير من صورة سلبية صغيرة أفضل من صورة بنفس الحجم تم التقاطها مباشرة فيما يتعلق بحدة التفاصيل. … يجب توخي الحذر للتمييز بين المزايا التي يمكن اكتسابها في التكبير من خلال استخدام عدسة أصغر ، مع العيوب التي تنتج عن تدهور القيم النسبية للضوء والظل.

تايلور 1892

يتذكر جون تريل تايلور صيغة الكلمة هذه لنوع من المسافة البؤرية:[5]

لقد رأينا أنه تم وضعه كقاعدة تقريبية من قبل بعض الكتاب في مجال البصريات (توماس ساتون ، إذا تذكرنا جيدًا) ، أنه إذا كان قطر نقطة التوقف جزءًا أربعين من تركيز العدسة ، فإن عمق التركيز سيتراوح بين اللانهاية والمسافة تساوي أربعة أضعاف الأقدام التي توجد في بؤرة العدسة.

تشير هذه الصيغة إلى معيار مدونة قواعد سلوك أكثر صرامة مما نستخدمه عادة اليوم.

هودجز 1895

يناقش جون هودجز عمق المجال بدون صيغ ولكن مع بعض هذه العلاقات:[6]

ومع ذلك ، هناك نقطة يكون بعدها كل شيء في تعريف جيد تصويريًا ، ولكن كلما طالت مدة تركيز العدسة المستخدمة ، كلما زادت النقطة التي يكون بعدها كل شيء في بؤرة حادة ستتم إزالتها من الكاميرا. من الناحية الحسابية ، يختلف مقدار العمق الذي تمتلكه العدسة عكسيًا حسب مربع تركيزها.

تشير هذه العلاقة التي تمت ملاحظتها “رياضيًا” إلى أن لديه معادلة في متناول اليد ، ومعلمات برقم f أو “نسبة شدة” فيها. للحصول على علاقة مربعة عكسية مع الطول البؤري ، عليك أن تفترض أن حد CoC ثابت وأن قطر الفتحة يتساوى مع الطول البؤري ، مما يعطي رقمًا بؤريًا ثابتًا.

بايبر 1901

قد يكون C. Welborne Piper أول من نشر تمييزًا واضحًا بين عمق الميدان بالمعنى الحديث و عمق التعريف في المستوى البؤري ، ويعني ذلك عمق التركيز و عمق المسافة تستخدم أحيانًا للأول (في الاستخدام الحديث ، عمق التركيز عادة ما تكون محجوزة لهذا الأخير).[7] يستخدم المصطلح عمق ثابت إلى عن على ح، ويقيسها من البؤرة الرئيسية الأمامية (على سبيل المثال ، يحسب بُعدًا بؤريًا واحدًا أقل من المسافة من العدسة للحصول على صيغة أبسط) ، وحتى يقدم المصطلح الحديث:

هذا هو أقصى عمق ممكن للمجال ، و ح + F يمكن تحديد مسافة أقصى عمق للمجال. إذا قمنا بقياس هذه المسافة خارج البؤرة فإنها تساوي ح، وتسمى أحيانًا المسافة البؤرية. ثابت العمق والمسافة البؤرية مميزة تمامًا ، على الرغم من أنهما لهما نفس القيمة.

من غير الواضح ما هو التمييز الذي يقصده. وبجوار الجدول الأول في ملحقه ، يلاحظ كذلك:

إذا ركزنا على اللانهاية ، فإن الثابت هو المسافة البؤرية لأقرب كائن موضع التركيز. إذا ركزنا على مسافة بؤرية إضافية تساوي الثابت ، فإننا نحصل على أقصى عمق للمجال من نصف المسافة الثابتة تقريبًا إلى اللانهاية. الثابت إذن هو المسافة البؤرية الفائقة.

في هذه المرحلة ليس لدينا دليل على المصطلح فرط البؤرة قبل بايبر ، ولا الواصلة مفرط البؤرة الذي استخدمه أيضًا ، لكن من الواضح أنه لم يدعي أنه يصوغ هذا الوصف نفسه.

دير 1906

قد يكون لويس دير أول من حدد بوضوح التعريف الأول ،[8] التي تعتبر صحيحة تمامًا في العصر الحديث ، ولاشتقاق الصيغة المقابلة لها. باستخدام ص للمسافة البؤرية ، د لقطر الفتحة ، د للقطر الذي لا يجب أن تتجاوزه دائرة الارتباك ، و F بالنسبة للبعد البؤري ، يستمد:ف = { فارك {(د + د) و} {د}}[1]

كقطر الفتحة ، د هي نسبة البعد البؤري ، F إلى الفتحة العددية ، ن؛ وقطر دائرة الارتباك ، ج = د، هذا يعطي معادلة التعريف الأول أعلاه.p = { frac {({ tfrac {f} {N}} + c) f} {c}} = { frac {f ^ {2}} {Nc}} + f

جونسون 1909

يستخدم جورج ليندسي جونسون المصطلح عمق الميدان لما يسميه أبني عمق التركيز ، و عمق التركيز بالمعنى الحديث (ربما لأول مرة) ،[9] كخطأ المسافة المسموح به في المستوى البؤري. تشمل تعريفاته المسافة البؤرية:

عمق التركيز هو مصطلح مناسب ، ولكنه ليس دقيقًا تمامًا ، يستخدم لوصف مقدار حركة الأرفف (للأمام أو للخلف) التي يمكن إعطاؤها للشاشة دون أن تصبح الصورة غير واضحة بشكل معقول ، أي بدون أي تشويش في الصورة يتجاوز 1 / 100 بوصة ، أو في حالة الصور السلبية المراد تكبيرها أو العمل العلمي ، 1/10 أو 1/100 مم. ثم عرض نقطة الضوء ، والتي ، بالطبع ، تسبب ضبابية على كلا الجانبين ، أي 1/50 بوصة = 2ه (أو 1/100 بوصة = ه).

يوضح رسمه أن له ه هو نصف قطر دائرة الارتباك. لقد توقع بوضوح الحاجة إلى ربطه بحجم التنسيق أو التكبير ، لكنه لم يقدم مخططًا عامًا لاختياره.

عمق المجال هو بالضبط نفس عمق التركيز ، فقط في الحالة الأولى يتم قياس العمق بحركة اللوحة ، ويتم تثبيت الكائن ، بينما في الحالة الأخيرة يقاس العمق بالمسافة التي يمكن للكائن من خلالها تتحرك دون أن تتجاوز دائرة الارتباك 2ه.

وبالتالي ، إذا كانت العدسة التي تركز على اللانهاية لا تزال تعطي صورة حادة لجسم على بعد 6 ياردات ، فإن عمق مجالها من اللانهاية إلى 6 ياردات ، كل كائن يتجاوز 6 ياردات يكون في بؤرة التركيز.

هذه المسافة (6 ياردات) تسمى مسافة فائقة البؤرة للعدسة وأي قرص تشويش مسموح به يعتمد على البعد البؤري للعدسة وعلى المحطة المستخدمة.

إذا كان حد الارتباك نصف القرص (أي ه) على أنها 1/100 بوصة ، ثم المسافة البؤريةH = { frac {Fd} {e}},

د كونها قطر المحطة ، …

استخدام جونسون ل السابق و الأخير يبدو أنه تم تبديله ؛ ربما السابق هنا للإشارة إلى عنوان القسم السابق مباشرة عمق التركيزو و الأخير إلى عنوان القسم الحالي عمق الميدان. باستثناء خطأ عامل 2 الواضح في استخدام نسبة قطر التوقف إلى نصف قطر CoC ، فإن هذا التعريف هو نفسه مسافة Abney فائقة البؤرة.

آخرون ، أوائل القرن العشرين

المصطلح مسافة فائقة البؤرة يظهر أيضًا في Cassell’s موسوعة عام 1911 ، دليل سنكلير للتصوير عام 1913 ، وبايلي المصور الكامل عام 1914.

كينغزليك 1951

رودولف كينجسليك صريح في معنيين:[1]

إذا كانت الكاميرا تركز على مسافة س يساوي 1000 ضعف قطر فتحة العدسة ، ثم العمق البعيد د_ {1} يصبح لانهائي. مسافة الجسم الحرجة هذه “ح“المعروف باسم المسافة البؤرية. بالنسبة للكاميرا التي تركز على هذه المسافة ، D_ {1} = infty و د_ {2} = ح / 2، ونرى أن نطاق المسافات المقبولة في التركيز البؤري سوف يمتد من نصف المسافة البؤرية إلى اللانهاية. وبالتالي ، فإن المسافة البؤرية هي أكثر مسافة مرغوبة لضبط بؤرة الكاميرا ذات التركيز الثابت مسبقًا. وتجدر الإشارة أيضًا إلى أنه إذا تم التركيز على الكاميرا ق = infty، أقرب كائن مقبول في L_ {2} = sh / (h + s) = h / (h / s + 1) = h (بالمعادلة 21). هذا هو المعنى الثاني المهم للمسافة البؤرية.

يستخدم Kingslake أبسط الصيغ لـ DOF للمسافات القريبة والبعيدة ، والتي لها تأثير في جعل التعريفين المختلفين للمسافة البؤرية يعطيان قيمًا متطابقة.

الطول البؤري وزاوية الرؤية والمنظور
الطول البؤري

يكون الطول البؤري، أو نطاق الطول البؤري في حالة الزووم، عادة الاهتمام الأول عند اختيار عدسة لصورة معينة أو نوع معين من التصوير الفوتوغرافي. ويحدد الطول البؤري لأي عدسة خاصيتين هامتين للمصورين الفوتوغرافيين: التكبير وزاوية الرؤية.

تتوافق الأطوال البؤرية الأطول مع التكبير الأعلى والعكس. وتتمتع العدسات عريضة الزاوية ذات الأطوال البؤرية القصيرة بقدرة تكبير أقل، مما يعني أنه يتعين عليك الاقتراب فعليًا من هدف متوسط الحجم لكي تملأ الإطار. لكن هذا يعني أيضًا أنه يمكنك وضع أهداف كبيرة في الإطار بدون الاضطرار للتصوير من مسافة بعيدة. وتتمتع العدسات المقربة ذات الأطوال البؤرية الطويلة بقدرة تكبير أعلى، لذا يمكنك ملء الإطار بأهداف بعيدة عن الكاميرا.

تعريف تقني للطول البؤري – حديث تقني:

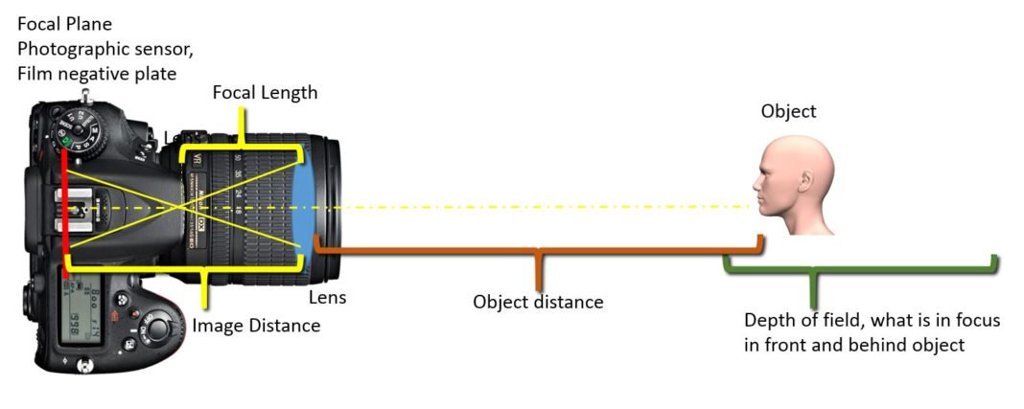
يتم تعريف الطول البؤري للعدسة بأنه المسافة من نقطتها الرئيسية الثانوية إلى نقطتها البؤرية الخلفية عند تعيين البؤرة على ما لا نهاية. وتعد النقطة الرئيسية الثانوية واحدة من ست “نقاط رئيسية” يتم استخدامها كنقاط مرجعية في عدسة بصرية (النقطتان البؤريتان الأمامية والخلفية، والنقطتان العقديتان الأساسية والثانوية، والنقطتان الرئيسيتان الأساسية والثانوية). ولا يوجد موقع محدد مسبقًا للنقطة الرئيسية الثانوية في عدسة مركبة، حيث يمكن أن تكون في مكان ما داخل ماسورة العدسة أو في نقطة ما خارج الماسورة، حسب تصميم العدسة، لذلك لا توجد طريقة سهلة لقياس الطول البؤري لعدسة ما بنفسك بشكل دقيق.

الطول البؤري وزاوية الرؤية:

تصف “زاوية الرؤية” مقدار ما سيتم التقاطه من المشهد أمام الكاميرا بواسطة حساس الكاميرا. وبمصطلحات تقنية بعض الشيء، فإن هذا هو النطاق الزاوي للمشهد الذي يتم التقاطه على الحساس، ويقاس قطريًا. ولكن من المهم أن نتذكر أن زاوية الرؤية تتحدد بأكمله بواسطة كل من الطول البؤري للعدسة وتنسيق حساس الكاميرا، لذلك ستكون زاوية الرؤية التي تحصل عليها من أي عدسة معينة مختلفة على كاميرات الإطار الكامل 35 مم وتنسيق APS-C. وسوف تتمتع العدسات المختلفة ذات الطول البؤري المتساوي دائمًا بنفس زاوية الرؤية عند استخدامها مع حساس بنفس الحجم.

المنظور:

مع الأطوال البؤرية الطويلة، سوف تبدو الأهداف في المقدمة والخلفية في الغالب أقرب من بعضها البعض في الصورة النهائية. ويسمى هذا التأثير أحيانًا “ضغط الصورة المقربة”، رغم أنها ليست ناتجة في الواقع بواسطة العدسة نفسها. وما يحدث في الواقع هو أنه عند استخدام عدسة مقربة، فإنك ستحتاج للابتعاد عن أهدافك. ولذلك، بالنسبة للمسافة من الكاميرا إلى الأهداف في المقدمة والخلفية، فهي في الواقع قريبة من بعضها. وتوجد طريقة أخرى للتعبير عن ذلك: بما أن الأهداف في المقدمة والخلفية على مسافة بعيدة كثيرًا من الكاميرا، فإن أحجامها النسبية في الصورة النهائية ستكون أقرب إلى الواقع. وعند التصوير باستخدام عدسة عريضة الزاوية، تحتاج عادة إلى الاقتراب من الهدف الموجود في المقدمة بحيث يكون كبيرًا بما فيه الكفاية في الإطار، وهذا هو السبب الذي يجعل الأشياء البعيدة تبدو أصغر نسبيًا. ويكون الفرق في المنظور الواضح في الواقع نتيجة لمدى بعدك عن هدفك.

صورة بطول بؤري 300 مم
صورة بطول بؤري 24 مم
تمرين تطبيقي : المسافة البؤرية - قوة العدسة - YouTube
مدونة تفردوت للفيزياء: العدسات الرقيقةقياس وتعريف البعد البؤري في كاميرات DSLR | 2021
ρнσтσgяαρну /2/ 📷 | عالم المعلوماتية | Amino Amino

المراجع

PROMOTED CONTENT

6 Reasons Sharks Are Afraid Of DolphinsBrainberriesحسابات تيك توك هذه هي الأفضل بكل بساطةBrainberriesما الذي يخبأه ماضي ملكة الأردنHerbeautyلم يعرف أحد هذه المعلومات عن ملك الأردنBrainberries

  1. ^ أ ب Kingslake ، رودولف (1951). العدسات في التصوير: الدليل العملي للبصريات للمصورين. جاردن سيتي ، نيويورك: مطبعة جاردن سيتي.
  2. ^ أ ب ساتون ، توماس ؛ داوسون ، جورج (1867). معجم التصوير الفوتوغرافي. لندن: سامبسون لو ، سون ومارستون.
  3. ^ البصريات في التصوير الفوتوغرافي – كتب جوجل. تم الاسترجاع 24 سبتمبر 2014.
  4. ^ أبني ، دبليو دي دبليو (1881). رسالة في التصوير الفوتوغرافي (الطبعة الأولى). لندن: Longmans ، Green ، and Co.
  5. ^ تايلور ، جيه تريل (1892). بصريات التصوير الفوتوغرافي وعدسات التصوير. لندن: ويتاكر وشركاه.
  6. ^ هودجز ، جون (1895). عدسات التصوير الفوتوغرافي: كيف تختار ، وكيف تستخدم. برادفورد: بيرسي لوند وشركاه.
  7. ^ بايبر ، سي ويلبورن (1901). أول كتاب للعدسة: رسالة أولية عن عمل واستخدام العدسة الفوتوغرافية. لندن: هازل وواتسون وفايني.
  8. ^ دير ، لويس (1906). التصوير الفوتوغرافي لطلاب الفيزياء والكيمياء. لندن: ماكميلان.
  9. ^ جونسون ، جورج ليندسي (1909). البصريات الفوتوغرافية والتصوير الملون. لندن: Ward & Co.

روابط خارجية

PROMOTED CONTENT

ما تريده المرأة: 7 صفات للرجال تحتاجها كل امرأةLimelight Media6 Reasons Sharks Are Afraid Of DolphinsBrainberriesأثارت هذه الصورة ضجة كبيرة على كل مواقع التواصل الاجتماعيLimelight Media

من فريد ظفور

مصور محترف حائز على العديد من الجوائز العالمية و المحلية في مجال التصوير الفوتوغرافي.

مقالة ذات صلة

التراث اللامادي مسابقات التصوير

تُطلق جائزة حمدان بن محمد للتصوير (هيبا). دورتها الثالثة عشرة بعنوان “الاستدامة”

فريد ظفور
التراث اللامادي مسابقات التصوير

شاركوا جائزة حمدان للتصوير (هيبا) في بالمحور العام (الأبيض والأسود) .أحد محاور الدورة الثالثة عشرة…

فريد ظفور
التراث اللامادي فوتوغرافيا الأربعاء

كتبت جائزة حمدان (هيبا) في فوتوغرافيا.. .صورة حارس مقبرة إخناتون ..كريم بدر يكشف القصة.

فريد ظفور

فاتك

بدون تصنيف

ندعوكم للمشاركة بجائزة حمدان للتصوير بدورة:الإستدامة. حتى 30 يونيو 2024م. للدورة الثالثة عشرة.

بدون تصنيف

تعرفوا معنا ماهو الأنبوب الامتدادي؟ ​​​​​​​What is an Extension Tube – إعداد: غدير معروف

بدون تصنيف

كتبت جائزة حمدان الدولية للتصوير ( هيبا ) في فوتوغرافيا …. وثائق لدراسة السلوك الإنساني (1-2)

بدون تصنيف

كتبت جائزة حمدان الدولية للتصوير ( هيبا ) في فوتوغرافيا ..تشريعات القانون تتصدّى لتزييف الفوتوغراف