عدد غراهام
من ويكيبيديا،
عدد غراهام الذي سمي باسم رونالد غراهام، هو عدد كبير وهذا هو الحد الأعلى لحل المسائل الرياضية في نظرية رامزي.
هذا العدد اكتسب درجة عالية من الموثوقية الشعبية عندما وصفه مارتن غاردنر في قسم “الألعاب الرياضية” من مجلة العلوم في نوفمبر تشرين الثاني عام 1977، حيث كتب أن “في دليل غير منشور، لغراهام أنشأه مؤخرا … أن ارتباطا يقفز مساحات بأنه يحمل الرقم القياسي لأكبر عدد أستخدم مطلقا منذ أى وقت مضى في البراهين الرياضية المعقدة “. أى في كتاب غينيس للارقام القياسية العالميةفي عام 1980 مع تكرار المطالبة من جانب جاردنر، إضافة إلى الاهتمام الشعبي لهذا العدد. وفقا للفيزيائي جون بايز، ابتكر غراهام القيمة المعروفة الآن بعدد غراهام في محادثة مع غاردنر نفسه. بينما كان غراهام يحاول شرح النتيجة في نظرية رامزي التي كان قد استمدها مع BL روتشيلد الذي تعاون معه، ووجد أن قيمة غراهام المعروفة الآن بعدد غراهام أسهل للشرح من العدد الفعلي الذي يظهر في الإثبات لأن الرقم الذي وصفه غراهام لغاردنر هو أكبر من الرقم في الورقة نفسها، وكلاهما يمثلان الحدود العليا الصالحة لإيجاد حل لمعضلات نظرية رامسي التي يدرسها غراهام وروتشيلد.[1]
عدد غراهام هو رقم كبير أكبر بشكل لا يمكن تصوره أكبر من أى من الأعداد الكبيرة المعروفة مثل جووجل، جووجل بلكس، وحتى أكبر من رقم سكيويز و رقم موزر. في الواقع، مثل الثلاثة الأخيرة من هذه الأرقام، و ملاحظتها الكون هو أبعد ما يكون صغيرا جدا لبقعة عادية التمثيل الرقمي من عدد غراهام، على افتراض أن كل رقم يحتل وحدة واحدة حجم بلانك.حتى أبراج الطاقة من النموذج {\displaystyle \scriptstyle a^{b^{c^{\cdot ^{\cdot ^{\cdot }}}}}}
الأعداد الصحيحة المحددة المعروفة تكون أعظم بكثير من عدد غراهام وقد ظهرت في العديد من البراهين الرياضية الخطيرة (على سبيل المثال، في اتصال مع أشكال مختلفة من نهايات فريدمان نظرية كروسكال).
السياق
مثال مكعب ثلاثى الأبعاد ثنائى اللون تحتوي على one single-coloured 4-vertex coplanar complete subgraph. يظهر رسم بياني ثانوي أدنى المكعب. لاحظ أن هذا المكعب سوف لا يحتوي على مثل هذا التمثيل البياني الثانوي إذا، استعيض عن الحافة السفلية على سبيل المثال، في التمثيل البياني الثانوي الحاضر بحافة زرقاء – مما يثبت بالدليل أن N *> 3
.ويرتبط عدد غراهام للمشكلة التالية في نظرية رامزي:
رقم غراهام ينسب إلى “رونالد غراهام” في نظرية “رامزي” ويشكل قيمة أسية كبيرة لعدد. واشتهر هذا الرقم بين العامة في عام 1977 عندما كتب عنه أحد الرياضيين واصفاً إياه بأنه: “أضخم رقم في العالم تم استخدامه في إثبات رياضي”.
رقم غراهام يتخطى بكثير جداً أعلى الأرقام في العالم مثل جوجول وجوجول-بلكس أو سكيويز، ومن الصعب جداً تمثيل رقم غراهام كتابة لأنه يتمثل من عدد ذو قيمة أسية، والقيمة الأسية بدورها لها قيمة أسية أخرى، وهكذا دواليك (مثل: 5×10^8^500^845^1215… حيث تمثل علامة ^ الأُس) وحتى مثل هذا التمثيل يعتبر غير ذو جدوى للتعبير عن الرقم في شكله العلمي الصحيح. لاحقاً، ظهرت أرقاماً صحيحة أكبر من من رقم غراهام وتعدته بكثير أيضاً، في إثباتات رياضية جادة جداً (كمعادلة فريدمان وأعداد النهاية في نظرية كروسكال).
كانت المسألة الحسابية التي حاول غراهام حلها وكانت سبباً في هذا الرقم ما يلي: إذا كان لديك مضلعاً هائل العدد من الأضلاع (عدد الرؤوس في المضلع = ن)، ثم صل كل نقطتين فيه بخط، ليكون لديك مضلع عدد أضلاعه = 2^ن، ثم قم بتلوين كل ضلع إما باللون الأزرق أو الأحمر. فما هي أقل قيمة للمتغير (ن) بحيث يمكنك الحصول على وجه (مستطيل في المضلع) كافة أضلاعه ملونة بلون واحد (إما كلها زرقاء أو كلها حمراء). استطاع غراهام في النهاية أن يثبت أن هذه المسألة قابلة للحل وكانت حل المسألة هو (رقم غراهام). أمكن التعبير عن رقم غراهام في المجلة العلمية الأمريكية في مقال لمارتن جاردنر بطريقة “تدوين نوث الصاعد” على الشكل الموضح أدناه في الصورة.
أما الأرقام الموضحة أدناه فهي آخر 500 رقم على أقصى اليمين من عدد أو رقم غراهام: …02425950695064738395657479136519351798334535362521
43003540126026771622672160419810652263169355188780 38814483140652526168785095552646051071172000997092 91249544378887496062882911725063001303622934916080 25459461494578871427832350829242102091825896753560 43086993801689249889268099510169055919951195027887 17830837018340236474548882222161573228010132974509 27344594504343300901096928025352751833289884461508 94042482650181938515625357963996189939679054966380 03222348723967018485186439059104575627262464195387

تعريف
باستخدام تدوين نوسز-للسهم الأعلى، عدد غراهام G (على النحو المحدد في مقال جاردنر المجلة العلمية الأمريكية ) هو{\displaystyle \left.{\begin{matrix}G&=&3\underbrace {\uparrow \uparrow \cdots \cdots \cdots \cdots \cdots \uparrow } 3\\&&3\underbrace {\uparrow \uparrow \cdots \cdots \cdots \cdots \uparrow } 3\\&&\underbrace {\qquad \;\;\vdots \qquad \;\;} \\&&3\underbrace {\uparrow \uparrow \cdots \cdot \cdot \uparrow } 3\\&&3\uparrow \uparrow \uparrow \uparrow 3\end{matrix}}\right\}{\text{64 layers}}}
عدد غراهام Grahm number (واللفظ الصحيح هو عدد غرام) نسبة لعالم الرياضيات رون غراهاموعدد غراهام هو أكبر عدد تم استخدامه يوما لإثبات مبرهنة رياضيةولكن قبل ان نخوض في عدد غراهامعلينا اولا معرفة طريقة كتابة الاعداد الكبيرة وهذا ليس صعبا كما سترى،
كيف تكتب الاعداد الكبيرةيمكنك أن تكتب المليون هكذا 1000000 وللاختصار يمكن كتابته على شكل 106 يساوي 10 ×10 ×10×10 ×10 ×10(عشرة مضروبة بنفسها 6 مرات وليس 6×10)
| مليون | 1000000 | 106 |
| مليار | 1000000000 | 109 |
| جوجل | واحد وعلى يمينه 100 صفر | 10100 |
طبعا العدد الذي في الاس يمكن أن يكون عددا كبيرا أيضا ،10106هذا يساوي واحد وعلى يمينه مليون من الاصفار، ولن اقوم بكتابته بالطريقة التقليدية، وهنا يتضح لنا فائدة هذا الاسلوب في كتابة الارقام.
طريقة اخرى للكتابة هي باستخدام الاسهميمكنك أن تكتب 103 على هذا الشكل 3↑10 ويمكنك أن تكتب المليون على هذا الشكل 10 السهم هنا ببساطة يشير للقوة أو الاس
لكن ماذا عن الاعداد الاكبر من هذا بكثير ، لو أردنا كتابة الرقم التالي

لاشك أن كتابته ستكون صعبة جدا ولاتنسى أيضا صعوبة اجراء العمليات الحسابية عليهواحدة من الطرق ال مستخدة مايسمى
Tetration
وتشبه الطريقة السابقة ولكن بالمزيد من الاسهم 3 ↑↑10هذا يعني تكرار 10↑10 ثلاث مرات ( 10↑10) ↑10وبما أن 10↑10 تساوي 1010 اذا فان 3↑↑10 تساوي 101010لاحظ أن وجود السهمين بشير الى ان العدد الذي في اليسار سيتكرر على شكل “برج” ان جاز التعبير، وسيكون طول البرج نفس العدد الذي في اليمين، على هذا فإن

في الحقيقة من عند هذه النقطة تصبح الامور معقدة نوعا ما، لكن اذا استمريت في المتابعة أعدك أن الامر سيستحق العناء في النهاية، تخيل نفسك في مغامرة عقلية خلال الارقام
الان ماذا لو وضعنا ثلاثة أسهم؟ وهي طريقة صحيحة في الكتابة، فلنقل 3↑↑↑10، بنفس المنطق السابق يمكننا كتابته هكذا
(10↑↑10) ↑↑10
كما لاحظت يوجد نمط يتكرر ، كرر العدد الذي في اليسار بمقدار العدد الذي في اليمين.

نبدأ الان الانتقال الى عدد غراهامفي البداية عندنا g1وهو رقم محدد بعينه وليس طريقة للكنابةg1 = 3↑↑↑↑3 (رقم كبير جدا لاحظ الاسهم الاربعة)بتطبيق ما تعلمناه سابفاg1 = 3↑↑↑↑3 = 3↑↑↑3↑↑↑3) = 3 ↑ ↑ ↑ (3 ↑ ↑ (3 ↑↑3))

لأ أريد تحليل g1 أكثر من هذا ولكن قد وصلتك فكرة كم هو كبير الرقم g1
هناك أيضا g2 وهو رقم أضخم بكثير من g1ببساطة نأخذ العدد الكبير جدا الذي هو g1 وليس عدد الاسهم ولكن g1 بحقيقته ، ويكون ذلك العدد هو عدد الاسهم في g2

نكرر هذه العملية مرة أخرى فنأخذ العدد الكبير الناتج من g2 ويكون عدد الاسهم في g3

وهكذا نعيد العملية نفسها لنحصل على g4 وg5 وg6 ….وحتى g64وأخيرا وصلنا الى عدد غرامg64 هو عدد غراهام وهو عدد كبير بلاشك يستحيل تخيله
الى هنا ينتهي الجزء الصعب ، بقي أن نعرف بماذا يستخدم عدد غراهامانظر الى الشكل 1

يمثل مربع بأربعة أضلاع وخطين إضافـيـيـن قطريين لايصال كل زاوية بالاخرى فيكون المجموع ستة خطوط، المطلوب منا تلوين تلك الخطوط بلونبن فقط إما الاحمر أو الازرق، ولكن هناك شرط لصحة التلوين وهو أن لاتكون جميع الخطوط بنفس اللون وقد حققنا هذا الشرط فعلا في الشكل 1 وهو مربع داخل بعدين 2D، طول وعرض.
المكعب شكل ضمن ثلاثة ابعاد ،طول وعرض وارتفاع (شكل2)
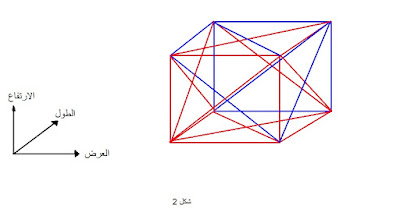
ويمكننا رسمه بنفس الشروط السابقة ففي النهاية المكعب يتكون من ستة مربعات ، وكل ما علينا فعله هو ضمان أن لاتكون الوجوه العمودية أو الافقية ذات أضلاع متشابهة اللون، لاحظ أننا نتحدث عن الوجوه العمودية أو الافقية ولاتهمنا الوجوه الداخلية القطرية.
وماذا لو حاولنا رسم الشكل بطريقة رباعية الابعاد؟ هل يمكن رسمه بنفس الشروط؟ والجواب هو نعم ونستطيع أيضا رسمه ضمن تلك الشروط بخمسة ابعاد وستة ابعاد أيضا وتستمر السلسلة حتى تصل الى عدد غرام من الابعاد ففي حالة محاولتك لرسم الشكل الهندسي السابق بعدد غرام من الابعاد فانك لن تتمكن من تلوينه بنفس الشروط وستحصل بلاشك على واجهة ملونة جميع اضلاعها بنفس اللون ، وهذا هو استخدام عدد غراهام في الرياضيات
رائع بلاشك أليس كذلك؟ وقد استحق العناءوبمكننا هنا ان نرى جمال الرياضيات وسحرها عدا اهميتها وتأثيرها المياشر وغير المباشر بالاخص الفيزياء وغيرها من العلوم الاخرى



